Контрольная работа: Математическое моделирование финансовых операций

Так как средняя относительная ошибка аппроксимации А меньше 5%, то модель точная.
3) Проверим адекватность модели.
а) Для адекватной модели характерно равенство математического ожидания ряда остатков 0. Проверка осуществляется на основе t-критерия Стьюдента. Расчеты произведем в табл. 1.4.
Таблица 1.4
Проверка адекватности модели
| Тп | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | -0,04 | 0,1139 | - | - | 0,0016 | - |
| 2 | -0,16 | 0,2093 | 0 | 0,0144 | 0,0256 | 0,0064 |
| 3 | -0,79 | 1,1827 | 1 | 0,3969 | 0,6241 | 0,1264 |
| 4 | 0,32 | 0,0005 | 1 | 1,2321 | 0,1024 | -0,2528 |
| 5 | 0,04 | 0,0663 | 1 | 0,0784 | 0,0016 | 0,0128 |
| 6 | 0,17 | 0,0163 | 0 | 0,0169 | 0,0289 | 0,0068 |
| 7 | 0,86 | 0,3164 | 1 | 0,4761 | 0,7396 | 0,1462 |
| 8 | -0,33 | 0,3938 | 1 | 1,4161 | 0,1089 | -0,2838 |
| 9 | 0,11 | 0,0352 | 0 | 0,1936 | 0,0121 | -0,0363 |
| 10 | 0,50 | 0,0410 | 1 | 0,1521 | 0,2500 | 0,0550 |
| 11 | -0,49 | 0,6202 | 1 | 0,9801 | 0,2401 | -0,2450 |
| 12 | 0,02 | 0,0770 | 0 | 0,2601 | 0,0004 | -0,0098 |
| 13 | 2,19 | 3,5816 | 1 | 4,7089 | 4,7961 | 0,0438 |
| 14 | 0,83 | 0,2836 | 1 | 1,8496 | 0,6889 | 1,8177 |
| 15 | 1,16 | 0,7439 | 1 | 0,1089 | 1,3456 | 0,9628 |
| 16 | 0,37 | 0,0053 | - | 0,6241 | 0,1369 | 0,4292 |
| 7,6870 | 10 | 12,5083 | 9,1028 | 2,7794 |
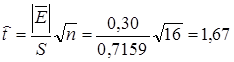
где
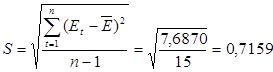
Сравним tрасч с табл t0,05 ; 15 = 2,13. Т.к. 1,67<2,13, то на уровне значимости α=0,05 гипотеза о том, что математическое ожидание ряда остатков Et=0 принимается.
б) Проверим условие случайности уровней остаточной компоненты по критерию пиков.
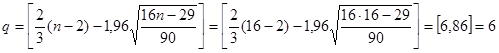
р=10, т.к. р>q (10>6), то условие случайности уровней остаточной компоненты выполняется.
в) Проверку независимости уровней ряда остатков (отсутствия автокорреляции) проведем с помощью критерия Дарбина-Уотсона. Расчеты произведем в табл. 1.4.
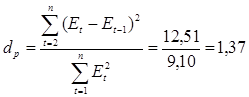
Т.к. d1 <dp =1,37=d2 , то для проверки независимости уровней ряда остатков используем первый коэффициент автокорреляции.
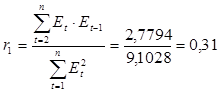
rтабл =0,34, так как r1 <rтабл (0,31<0,34), то автокорреляция уровней ряда остатков отсутствует.
г) Проверку соответствия ряда остатков нормальному закону распределения выполним по R/S-критерию.
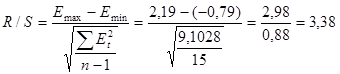
3 < 3,38< 4,21
d1 <R/S<d2 , значит условие подчинения ряда остатков нормальному закону распределения выполняется.
Так как все 4 условия выполнены, то модель является адекватной и ее можно использовать для прогнозирования.
4) Построим точечный прогноз на 4 шага вперед, т.е. на 1 год.
![]()
![]()
![]()
![]()
![]()
5) Отобразим на графике фактические, расчетные и прогнозные данные (Рис. 1).