Контрольная работа: Методика обработки экспериментальных данных 2
R = -561+805=244
2.2 Среднеарифметическое значение статистического ряда
![]()
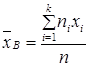 (2.2)
(2.2)
где ni – частота варианты xi ;
xi – варианта выборки;
n = ∑ ni – объем выборки;
Распределение выборки представлено в таблице 2.
Таблица 2
| Xi | n | Xi | n | Xi | n | Xi | n | Xi | n | Xi | n | Xi | n |
| -805 | 1 | -717 | 2 | -700 | 3 | -689 | 3 | -675 | 1 | -647 | 2 | -608 | 1 |
| -765 | 1 | -716 | 2 | -699 | 1 | -688 | 2 | -673 | 2 | -646 | 1 | -604 | 1 |
| -758 | 1 | -711 | 1 | -697 | 3 | -687 | 1 | -671 | 1 | -645 | 1 | -597 | 1 |
| -752 | 1 | -707 | 1 | -696 | 2 | -686 | 3 | -670 | 2 | -644 | 1 | -578 | 1 |
| -748 | 1 | -706 | 1 | -695 | 2 | -685 | 1 | -667 | 3 | -643 | 1 | -561 | 1 |
| -746 | 1 | -705 | 1 | -694 | 2 | -681 | 3 | -666 | 2 | -632 | 1 | ||
| -731 | 3 | -704 | 2 | -693 | 2 | -680 | 1 | -662 | 2 | -627 | 1 | ||
| -729 | 1 | -703 | 3 | -692 | 1 | -678 | 2 | -660 | 1 | -624 | 1 | ||
| -727 | 2 | -702 | 1 | -691 | 1 | -677 | 2 | -658 | 1 | -623 | 1 | ||
| -722 | 1 | -701 | 3 | -690 | 1 | -676 | 2 | -656 | 1 | -612 | 1 |
![]()
2.3 Оценка дисперсии
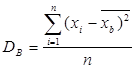
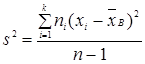 (2.3)
(2.3)
где s2 – несмещенная оценка генеральной дисперсии;
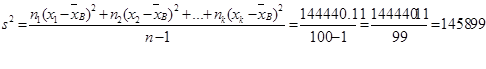
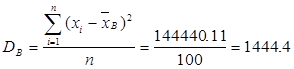
2.4 Оценка среднего квадратического отклонения
![]() (2.4)
(2.4)
![]()
2.5 Определение моды
Модой называют варианту с наибольшей частотой повторений.
Из таблицы 2 находим, что наибольшую частоту n =3имеют варианты x = -731, x = -703,x = -701,x = -700,x = -697, x = -689,x = -686, x = -681, x = -667.
2.6 Определение медианы
Если количество вариант число четное, то медиана вычисляется по формуле:
МВ =( xk + xk +1 )/2 (2.5.)
где xk – пятидесятый член вариационного ряда;
x k+1 – пятьдесят первый член вариационного ряда;
n – Количество вариант и n =2* k
МВ =( xk + xk +1 )/2=(-689–689)/2= -689
2.7 Расчет коэффициента вариации