Контрольная работа: Методика обработки экспериментальных данных 2
![]() (2.6)
(2.6)
![]()
Вывод:
Размах варьирования является простейшей характеристикой рассеяния вариационного ряда.
Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят сводные характеристики – генеральную дисперсию и средним квадратическим отклонением.
Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большее рассеяние, у которого коэффициент больше (эта величина безразмерная поэтому он пригоден для сравнения вариационных рядов, варианты которых имеют различную размерность.
В целом числовые характеристики служат для сравнения рассеяния вариационных рядов в сравнении с аналогичными числовыми характеристиками других вариационных рядов.
3. Построение полигона и гистограммы относительных частот
Для построения гистограммы и полигона относительных частот поделим вариационный ряд (табл. 1) на частичные интервалы. Результаты занесем в таблицу 3.
Таблица 3
|
Номер интервала I | Частичный интервал xi –xx +1 |
Сумма относительных частот wi |
Плотность частот
| |
| xi | xx +1 | |||
| 1 | -805 | -780,6 | 0,01 | 0,00041 |
| 2 | -780,6 | -756,2 | 0,02 | 0,00082 |
| 3 | -756,2 | -731,8 | 0,03 | 0,00123 |
| 4 | -731,8 | -707,4 | 0,12 | 0,00492 |
| 5 | -707,4 | -683 | 0,4 | 0,01639 |
| 6 | -683 | -658,6 | 0,24 | 0,00984 |
| 7 | -658,6 | -634,2 | 0,08 | 0,00328 |
| 8 | -634,2 | -609,8 | 0,05 | 0,00205 |
| 9 | -609,8 | -585,4 | 0,03 | 0,00123 |
| 10 | -585,4 | -561 | 0,02 | 0,00082 |
По таб. 3 строим гистограмму относительных частот (рис. 1).
Полигон получаем соединением вершин столбцов гистограммы. (рис. 1) Полигон получаем соединением вершин столбцов гистограммы.
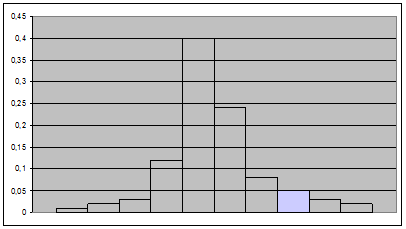


Рис 1.
Вывод: Полигон и гистограмму – графики статистического распределения строят для наглядности относительных частот в выборке.
4. Построение эмпирической функции распределения
Эмпирическая функция распределения выборки находится по формуле:
![]() (4.1)
(4.1)
где nx – число вариант меньших х ;
n – объем выборки.
По формуле (4.1) построим эмпирическую функцию распределения.