Контрольная работа: Методы решения алгебраических уравнений

Очевидно, что такими значениями служат:

а) и б) .

Для того, чтобы точка равновесия реализовалась на практике нужна её устойчивость, иначе малое возмущение может её быстро вывести из состояния, так что мы и ахнуть не успеем. Поэтому, исследуем эти состояния на устойчивость.

а) Рассмотрим сначала состояние равновесия , т.е. состояние, когда на вашем счету денег нет.д.обавим малое "возмущение" точке равновесия и исследуем её динамику со временем: т.е. , тогда из (25) получаем:

(27)

т.к , ясно, что поэтому ею можно пренебречь в (27). Вследствии имеем:

(29)

отсюда, легко получить, что

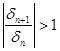(29)

т.е. возмущения нарастают со временем, что со своей стороны означает неустойчивость точки равновесия . По смыслу же, задачи это означает рост вклада со временем, если хоть какая-то малая сумма денег села на счёт.

б) Исследуем теперь устойчивость второй точки равновесия: . Здесь также дадим малое приращение к точке равновесия, т.е. рассмотрим значение и исследуем динамику этого состояния с течением времени n. Из (25) получаем:

(30)

Произведя преобразования, имеем:

Учитывая, что и поэтому, пренебрегая ею получаем:

(31)

для устойчивости точки равновесия , должно выполнятся условие:

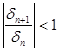(32)

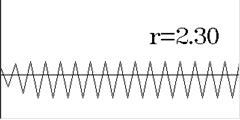
т.е.

(рис.1)

(33)

это условие со своей стороны означает, что

(34)

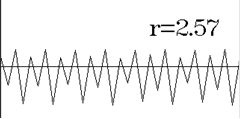
таким образом, если мы выберем в качестве относительного коэффициента роста:

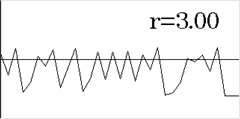
(рис.2)

(35)