Контрольная работа: Методы решения алгебраических уравнений

Таким образом, нелинейные итерационные формулы типа (2) скрывают в себе множество тайн и для их раскрытия нужны дополнительные исследования в каждом конкретном случае. Тем более, что не всегда удаётся оценить сходимость итерационного процесса глобально.

Этот пример хоть и является частным случаем формулы (2), но наводит на полезные размышления. Вышеизложенная итерационная формула (25) впервые была построена для изучения динамики популяций особей определённого вида в зависимости от истребления ареала пищи Ферхюльстом и носит его имя.

Мы видим, что одна и та же математическая модель может содержать в себе различные аспекты приложений, что вполне характерно для духа прикладной математики.

3. Методы решения алгебраических уравнений

Большинство задач физики, экономики, социологии, биологии и других областей знания приводят к решению алгебраических уравнений или систем уравнений.

Несмотря на наличие множества приближённых методов, в настоящее время, пожалуй, нет общего подхода для решения любого нелинейного уравнения и тем более нелинейной системы уравнений. Поэтому, в каждом частном случае приходится исследовать уравнения и строить соответствующие алгоритмы, комбинируя идеи разных численных методов. Так, что решение нелинейного уравнения, в настоящее время, скорее искусство, чем наука. Хотя, известные программные продукты современных фирм позволяют, во многих случаях, упростить поиск корней.

Перейдём на изложение основных известных и наиболее популярных методов. Прежде отметим, что при отыскании приближённых значений корней приходится решать две задачи:

а) отделение корней, т.е. отыскание достаточно малых областей в каждой из которых находится корень;

б) вычисление корней с заданной точностью.

3.1 Метод деления отрезка пополам (метод дихотомии)

Перед началом решения уравнения

(36)

мы должны выделить интервал поиска решения , т.е. ответить на вопрос а) предыдущего параграфа. Для этого используется теорема Вейерштрасса.

Теорема Вейерштрасса: Если на концах некоторого отрезка непрерывная функция принимает значения разных знаков, то на этом отрезке уравнение (36) имеет хотя бы один корень.

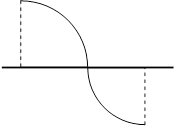
Эта теорема выражает геометрически очевидный факт (рис.4), состоящий в том, что если в точках и график непрерывной функции находится в

разных полуплоскостях от оси , то найдётся точка , такая что график этой функции пересекается с осью в точке , т.е. .

а bЗамечание: если при этом имеет первую

производную - не меняющую знака, то корень единственный.

Таким образом, мы можем сказать, что уже умеем

Рис. находить отрезок , где находится корень

уравнения (36), но этот отрезок можно уменьшать, основываясь на теореме Вейерштрасса.

Для этого в качестве первого приближения к корню берём середину отрезка , т.е.

(38)

Этой точкой отрезок делится на два равных отрезка: и . Используя теорему Вейерштрасса, устанавливаем в каком из этих отрезков лежит корень, т.е. на концах какого из этих двух отрезков функция принимает разные знаки. С этим отрезком действуем также, т.е. выбираем в качестве второго приближения к корню середину этого отрезка и продолжаем этот итерационный процесс, пока отрезок поиска решения не станет меньше требуемой точности .

Оценка погрешности вычислений по методу деления отрезка пополам производится по очевидной формуле:

(39)

Ясно, что , а относительная погрешность .

Изложенный метод легко программируется и даёт сходимость с точностью (39), хотя при практических вычислениях чаще пользуются комбинациями различных численных методов, добиваясь более быстрой сходимости процесса.

3.2 Метод ложного положения (метод хорд).

В основе метода лежит линейная интерполяция по двум значениям функции, имеющим противоположные знаки. Этот метод зачастую даёт более быструю сходимость, чем метод деления отрезка пополам.

Для иллюстрации алгоритма метода ложного положения (метода хорд), рассмотрим рис.5.