Контрольная работа: Модели и методы принятия решений
W(x3 ) = 0,1*1,0 + 0,2*0,5 + 0,3*0,0 + 0,2*2,4 + 0,2*3,2 = 1,32 ф.ст.
W(x4 ) = 0,1*1,5 + 0,2*1,0 + 0,3*0,5 + 0,2*0,0 +
+ 0,2*2,4 = 0,98 ф.ст. ← min
W(x5 ) = 0,1*2,0 + 0,2*1,5 + 0,3*1,0 + 0,2*0,5 + 0,2*4,8 = 1,86 ф.ст.
Минимальные ожидаемые возможные потери равны 0,98 ф.ст. в неделю, то есть наилучшее решение – шесть бочек в неделю.
6. Критерий Гурвица . ЛПР не располагает данными о спросе, поэтому ему нужно самому определить веса (коэффициент доверия) для исходов с низкими и высокими доходами. В данном случае из табл.7 самый низкий доход из возможных - при трех бочках в неделю, самый высокий - при семи. Из табл.6 и табл.7 следует, высокие доходы встречаются более, чем в одном исходе и с большей частотой. Принимаем коэффициент доверия а=0,5. Результаты расчетов приведены в таблице 13.
Таблица 13 – Критерий Гурвица
| Количество изготавливаемых бочек в неделю | Коэффициент доверия | Всего в неделю, ф.ст. | |
| а = 0,5 | (1 – а) = 0,5 | ||
| 3 | 1,2 | 1,2 | = 2,4 |
| 4 | 1,6 | 1,45 | = 3,05 |
| 5 | 2 | 1,7 | = 3,7 |
| 6 | 2,4 | 1,95 | = 4,35 |
| 7 | 2,8 | 2,2 | = 5 - максимум |
Если ЛПР использует указанные веса, то его решение по правилу Гурвица, будет состоять в том, чтобы семь бочек в неделю.
7. Критерий Лапласа . Для каждой строки матрицы доходов (табл.11) рассчитаем усредненный выигрыш и выберем максимальный.

W(x1 ) = 0,2*(2,4*5) = 2,4
W(x2 ) = 0,2*(2,9+3,2*4) = 3,14
W(x3 ) = 0,2*(3,4+3,7+4,0*3) = 3,82
W(x4 ) = 0,2*(3,9+4,2+4,5+4,8*2) = 4,44
W(x5 ) = 0,2*(4,4+4,7+5,0+5,3+5,5) = 4,98 - max
Решение, дающее максимальный средний доход, - изготавливать семь бочек.
8. Запас прочности (чувствительность) решений. Данные для определения зависимости выбора решения от изменений значений вероятностей рассчитаны в п.5 и п.7 и сведены в таблицу 14.
Таблица 14 - Зависимость выбора решения от изменений значений вероятностей
| Количество бочек изготавливаемых в неделю (возможные решения) | |||||
| 3 | 4 | 5 | 6 | 7 | |
| Заданные вероятности | 0,1 | 0,2 | 0,3 | 0,2 | 0,2 |
| Ожидаемый доход, ф.ст. | 2,4 | 3,17 | 3,88 | 4,5 | 5,06 |
| Альтернативные вероятности | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
| Ожидаемый доход | 2,4 | 3,14 | 3,82 | 4,44 | 4,98 |
Решение, дающее максимальный ожидаемый доход, - изготовлять семь бочек напитка, не претерпело изменений, однако средняя прибыль при равновероятности спроса снизилась с 5,06 ф.ст. до 4,98 ф.ст. в день. В данном случае выбор решения нечувствителен к незначительным изменениям вероятности, то есть не происходит замены выбранного варианта решений на новый.
9. Стоимость достоверной информации . Компания, например, принимает заказы па следующий неделю. Контролировать их количество не удается, однако можно, корректируя количество изготовляемых бочек, максимизировать доход. На число изготовляемых бочек теперь влияет число поступающих заказов. Если ежедневный спрос на бочки напитка будет точно совпадать с заказами, то максимальный ожидаемый доход можно по формуле рассчитать через математическое ожидание:
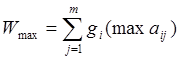
Используя данные табл.8 и табл.6
Wmax = 2,4*0,1 + 3,2*0,2 + 4,0*0,3 + 4,8*0,2 + 5,6*0,2 = 4,16 ф.ст.
Максимальный ожидаемый доход без дополнительной информации W(x5 ) = 5,06 ф.ст. (см.п.5).
Тогда стоимость достоверной информации равна:
4,16 - 5,06 = - 0,9 ф.ст.
Эта цифра равна минимальным ожидаемым возможным потерям (рассчитанным в п.5).
Таким образом, кондитерская может заплатить 0,9 ф.ст. в день, чтобы получать информацию о спросе.
Выводы :