Контрольная работа: Моделирование дискретной случайной величины по геометрическому закону распределения

n= 800 M= 695 P*= 0.869

n= 900 M= 801 P*= 0.890

n=1000 M= 908 P*= 0.908

n=1100 M= 990 Р*= 0.900

n=1200 M= 1102 P*= 0.918

n=1300 M= 1196 P*= 0.920

n=1400 M= 1303 P*= 0.931

n=1500 M= 1399 P*= 0.933

n=1600 M= 1487 P*= 0.929

n=1700 M= 1576 P*= 0.927

n=1800 M= 1691 P*= 0.939

n=1900 M= 1782 P*= 0.938

n=2000 M= 1877 P*= 0.939

Вероятность в опыте: p= 0.939

Теоретический расчёт вероятности работы цепи :

I способ :

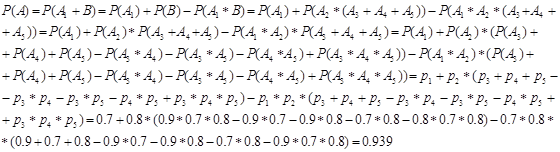
II способ :

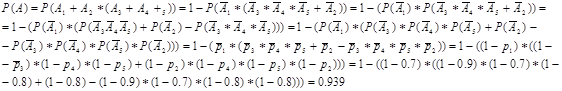
Вывод: Из математического моделирования с помощью TurboPascal видно, что частота появления события в серии опытов сходится по вероятности к рассчитанной теоретически вероятности данного события P(A) = 0.939.

Распределение дискретной случайной величины по геометрическому закону распределения

Моделирование случайной величины, имеющей геометрический закон распределения:

(X=xk) = p(1-p)^k

где x_k = k=0,1,2…, р – определяющий параметр, 0<p<1. Этот закон является дискретным. Составим теоретический ряд распределения, присваивая р=0,4 и k=0,1,2… и считая Р(Х=x_k ) получим теоретический многоугольник распределения, изображённый на рис.1.

По ряду распределения составим теоретическую функцию распределения F(x), изображённую на рис.2. Смоделируем дискретную случайную величину, имеющую геометрический закон распределения, методом Монте – Карло. Для этого надо:

1. Разбить интервал (0;1) оси ОК на k частичных интервалов:

D₁ – (0;р₁ ), D₂ – (р₁ ;р₁ +р₂ ) … D_k – (p₁ +p₂ +…+p_k-1 ;1)

2. Разбросать по этим интервалам случайные числа r_j из массива, смоделированного датчиком случайных чисел в интервале (0;1). Если r_j попало в частичный интервал D _I , то разыгрываемая случайная величина приняла возможное значение x_i .

По данным разыгрывания составим статистический ряд распределения Р*(Х) и построим многоугольник распределения, изображенный на рис.1. Построим статистическую функцию распределения F*(X), изображённую на рис.2. Теперь посчитаем теоретические и статистические характеристики дискретной случайной величины, имеющей геометрический закон распределения.