Контрольная работа: Моделирование дискретной случайной величины по геометрическому закону распределения

Рис.1.

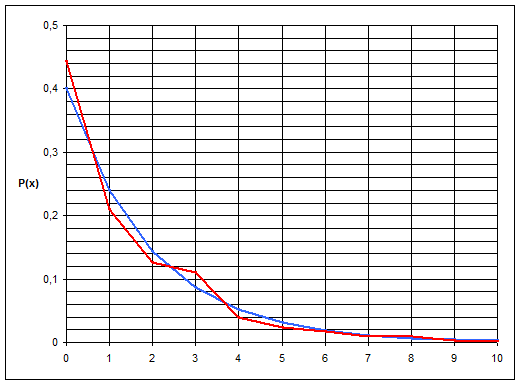
Рис.2.

Задание №2. Смоделируем случайную величину, имеющую геометрический закон распределения случайной величины

Программа в Turbo Pascal:

Program kursovik;

Uses crt;

Const M=300;

Var

K,I:integer;

P,SI,SII,SP,DTX,DSX,MX,MSX,GT,GS:real;

X:array[1..300] of real;

PI,S,P1,MMX,MS,D,DS,PS,STA,STR:ARRAY[0..10] OF REAL;

BEGIN;

CLRSCR;

randomize;

{ТЕОРЕТИЧЕСКИЙРЯД}

WRITELN('ТЕОРЕТИЧЕСКИЙ РЯД:');

P:=0.4; SI:=0;

FOR K:=0 TO 10 DO BEGIN

IF K=0 THEN PI[K]:=P ELSE

IF K=1 THEN PI[K]:=P*(1-P) ELSE

IF K=2 THEN PI[K]:=P*SQR(1-P) ELSE

IF K=3 THEN PI[K]:=P*SQR(1-P)*(1-P) ELSE

IF K=4 THEN PI[K]:=P*SQR(SQR(1-P)) ELSE

IF K=5 THEN PI[K]:=P*SQR(SQR(1-P))*(1-P) ELSE

IF K=6 THEN PI[K]:=P*SQR(SQR(1-P))*SQR(1-P) ELSE

IF K=7 THEN PI[K]:=P*SQR(SQR(1-P))*SQR(1-P)*(1-P) ELSE

IF K=8 THEN PI[K]:=P*SQR(SQR(SQR(1-P))) ELSE