Контрольная работа: Напрямки теорії ймовірностей та математичні дії над ними

1 . Основні напрямки теорії ймовірностей. Безпосередній підрахунок ймовірностей

Подією ( або випадковою подією) називається будь-який факт, що внаслідок експерименту може відбутися або не відбутися.

Ймовірністю події називається чисельна міра ступеня об'єктивної можливості цієї події. Ймовірність події А позначається .

Достовірною є подія , яка внаслідок експерименту неодмінно повинна відбутися:

.

Неможливою є подія, яка внаслідок експерименту не може відбутися:

.

Ймовірність будь-якої події знаходиться між нулем та одиницею:

.

Декілька подій утворюють повну групу, якщо внаслідок експерименту неодмінно повинна відбутися хоча б одна з них, тобто поява хоча б однієї з подій повної групи є достовірна подія.

Декілька подій в даному експерименті називаються несумісними , якщо поява однієї з них виключає появу іншої в одному і тому ж випробуванні.

Декілька подій є рівноймовірними , якщо немає підстав вважати яку-небудь з них більш можливою, ніж будь-яку іншу.

Кожний з можливих результатів випробування є елементарним наслідком. Вони утворюють повну групу, несумісні та рівноймовірні.

Елементарні наслідки є такими, що сприяють події , якщо поява цих виходів спричиняє появу події.

Відповідно до класичного визначення, ймовірність події обчислюється за формулою:

,

де – загальне число елементарних наслідків, – число наслідків, що сприяють події .

При безпосередньому підрахунку ймовірностей використовують основні формули та правила комбінаторики.

Перестановками є комбінації, що складаються з однакових елементів і відрізняються лише порядком розташування цих елементів. Число всіх перестановок дорівнює :

.

Розміщеннями є упорядковані комбінації, що складаються з m різних елементів даної n - елементної множини. Число розміщень дорівнює:

.

Сполученнями є неупорядковані комбінації, що складаються з m різних елементів даної n - елементної множини. Число сполучень дорівнює:

ймовірність теорія теорема байєс

.

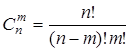Правило суми. Якщо деякий об'єкт А можна вибрати з сукупності об'єктів m способами, а інший об'єкт В може бути вибраний n способами, то вибрати або А, або В можна способами.

Правило множення . Якщо об'єкт А можна вибрати з сукупності об'єктів m способами, і після кожного такого вибору об'єкт В можна вибрати n способами, то пара об'єктів А і В може бути вибрана способами.

Приклад 1.

Кидають одночасно дві гральні кості. Знайти ймовірності таких подій:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--