Е_об = .

Вираз для енергії обертання сферичного ротатора аналогічний до такого для лінійної молекули. Виходячи з квантової теорії

Е_{об j} = .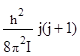

Тоді схема енергетичних рівнів для сферичного ротатора аналогічна до таких для лінійних молекул.

Різниця між цими рівнями буде у степені їх виродження, яка зв’язана, як відомо, з числом ступенів волі. Обертання лінійної молекули характеризується двома ступенями волі (j, m_j ), а обертання молекули типу сферичного ротатора характеризується трьома ступенями волі, а це задається трьома квантовими числами. Третім квантовим числом, крім j, m_j є k, яке визначає проекцію обертового моменту кількості руху на одну з рухомих осей. Напрямок цієї осі вибирається довільно, але ця вісь обов’язково обертається разом з молекулою. Проекція обертового моменту кількості руху на цю вісь вибирає квантове число k.

Молекули типу сферичної дзиги внаслідок високої симетрії не мають дипольного моменту і тому не можуть мати чисті спектри обертання, як поглинання, так і випромінювання.

Моменти інерції і обертові постійні молекул типу симетричного ротатору . Симетричні ротатори характеризуються двома рівними моментами інерції. Будемо позначати через а і с осі, які відповідають найменшому і найбільшому моменту інерції молекули, а через b – вісь, якій відповідає проміжковий або середній момент інерції. Тоді одержимо: І_а £ І_b £ І_с . Для симетричного ротатора можливі два випадки – витягнута дзига з виділеною віссю а і сплюснута дзига з виділеною віссю с. Для витягнутої дзиги І_а < І_b = І_с ; для сплюснутої – І_а = І_b < І_с . Таким чином, виділеною віссю (тобто віссю z) є вісь а найменшого моменту інерції для витягнутого ротатора і вісь с найбільшого моменту інерції для сплюснутого ротатора (мал.).

Трьом моментам інерції І_а , І_b , І_с відповідають три обертові постійні, які позначаємо А, В, С:

А = ; B = ; C = .

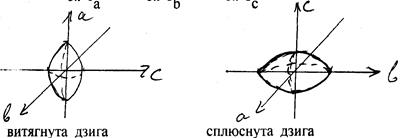
Для обертових постійних симетричного ротатора: витягнутого – А > B = С, сплюснутого – А = В > С.

Обертова енергія симетричного ротатора задається двома квантовими числами j і k. k – проекція повного обертового моменту кількості руху молекули на рухому вісь і набуває значення від – j до +j (2j + 1). Тоді: j = 0, 1, 2, 3…; k = 0, ±1, ±2….

Степінь виродження енергетичних рівнів симетричного ротатора q_{j , k} = 2 (2j + 1), тоді заселеність енергетичних рівнів:

.

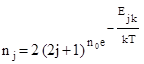Правила відбору (дозволені переходи між комбінуючими енергетичними рівнями) Δj = ±1; Δk = 0.

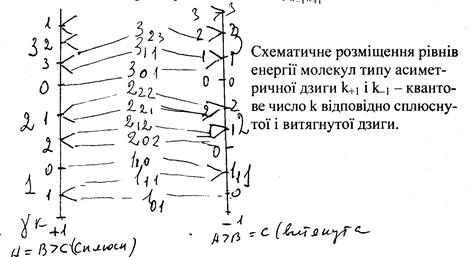
Система енергетичних рівнів симетричного ротатора визначається двома квантовими числами. Схема розміщення цих рівнів для витягнутого і сплющеного ротатора приведена на мал.

Якщо врахувати центробіжні сили між ядрами, то для

Е_jk = 2Bj (j + 1) – 4Dj (j +1)³ – 2D_jk (j + 1) k² .

Спектри обертання молекул типу асиметричного ротатора

Для молекул типу асиметричного ротатора всі три моменти інерції різні: І_а < І_b < І_с і відповідно A > B > C. Характер асиметрії може бути виражений через параметр асиметрії Х = .

Для витягнутої дзиги: А > B = C, тобто В = С: Х = . Для сплющеної дзиги: А = В > C: Х = . Найбільшою асиметрією володіють молекули з Х= 0, при цьому В = , тобто обертове постійне В є середньою між А і С. Енергетичні рівні асиметричної дзиги описуються рівнями:

,

– функція параметра асиметрії Х.

Для кожного j існує 2j + 1 значення функції , що задаються числом τ, яке набуває двох значень: – j до +j. Правила відбору: Δj = 0, ±1. Дотримується правило неперетинання ліній підрівнів з одинаковим числом j.

Для симетричних дзиг спостерігається двократне виродження по квантовому числу k. Для кожного j підрівнів 2j + 1. Перше число в індексі енергетичного рівня показує квантове число витягнутої дзиги, а друге – сплющеної. Наприклад, 2₀₂ – j = 2; k_–1 = 0; k₊₁ = 2. Індекси –1 і +1 є параметрами Х. Повне: ; τ = k_–1 – k₊₁ .

Коливання молекул. Коливні спектри . Коливні спектри молекул вивчаються методами інфрачервоної спектроскопії. Ці спектри зв’язані з переходами між коливними енергетичними станами або з класичної точки зору з коливанням атомних ядер відносно рівноважних положень. Число і частоти смуг залежать від числа атомів, що входять до складу молекули, від мас ядер, від геометрії і симетрії молекул і від потенціального поля внутрімолекулярних сил. Інтенсивність спектра визначається дипольним моментом і поляризуємістю. По коливним спектрам спектрам проводять структурні дослідження, визначають симетрію молекули та наявність тих чи інших функціональних груп.

Коливні спектри молекул . Коливні спектри можна вивчати для речовин в будь-якому агрегатному стані – твердому, рідкому чи газоподібному. При розгляді коливного руху молекул в спектроскопії широко використовується поняття про криві потенціальної енергії – u(r). Слід підкреслити, що для коливного руху ядер роль потенціальної енергії відіграє повна (тобто потенціальна і кінетична) енергія електронів. При зміщенні ядер положення рівноваги сили хімічного зв’язку намагаються вернути їх у вихідне положення. Оскільки хімічний зв’язок визначається рухом електронів, то природно, що сила, яка повертає ядро у вихідне положення виникає за рахунок зміни повної енергії електронів, яка обумовлюється зміною взаємного положення ядер, для яких в свою чергу вказана енергія має зміст потенціальної енергії u(r).