Контрольная работа: Общий курс высшей математики

Решение:

Если приращение аргумента ∆х = х₁ – х₀ достаточно мало по абсолютной величине, то приращение функции ∆f = f (x₁ ) – f (x₀ ) приближенно равно дифференциалу функции df. Поэтому справедлива формула

f (x₀ + _∆ x) ≈ f (x₀ ) + f^/ (x₀ ) _∆ x.

Для вычисления приближенного значения функции у = ln в точке х₁ = 0,013 вычислим производную этой функции в точке х₀ = 0:

f^/ (x) = ==

==

f^/ (x) = f^/ (0) = ==-1

Подставив в формулу получим; f(0,013) =-0,013

Ответ: -0,013

Задание 96

Исследовать функцию и построить ее график.

Решение

1. Область определения данной функции – вся числовая ось, то есть интервал (-∞; +∞), так как выражение

f (x) =

в правой части аналитического задания функции имеет смысл при любом действительном х .

2. Как элементарная функция, данная функция является непрерывной в каждой точке своей области определения, то есть в каждой точке числовой оси.

3. Найдем все асимптоты графика данной функции.

Вертикальных асимптот график данной функции у = f (x) не имеет, поскольку последняя непрерывна на всей числовой оси формула

Для отыскания наклонной асимптоты при х→ +∞ вычислим следующие два предела k = limy/xи b = lim (y – kx)

Если оба они существуют и конечны, то прямая у = kx + bявляется наклонной асимптотой при х→+∞ графика функции у = f (x)

Прежде чем обращаться к вычислению указанных пределов, напомним тождество √х² = |х| (1), из которого следует, что при x > 0 √х² = х ,

а при х < 0 √х² = -х или х = -√х² (2)

Приступая к вычислению первого предела, разделим числитель и знаменатель дроби на х² , затем воспользуемся равенством (1) и основными свойствами предела:

k======

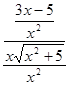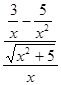==0

Для вычисления второго предела разделим числитель и знаменатель дроби на х и, действуя далее аналогично тому, как и при вычислении первого предела, получим:

b =(y – kx)= y == =

===3

Следовательно, прямая у = 3 является наклонной асимптотой графика данной функции при х→+∞ (поскольку угловой коэффициент k этой прямой равен нулю, то такую наклонную асимптоту называют также горизонтальной при х→+∞.

Для отыскания наклонной асимптоты при х→ -∞ вычислим пределы k₁ = limy/xи b₁ = lim (y – kx)