Контрольная работа: Прогноз среднего значения цены

Магазин торгует подержанными автомобилями. Статистика их потребительских цен накапливается в базе данных. В магазин пригоняют на продажу очередную партию небольших однотипных автомобилей. Как назначить их цену? Статистический подход позволяет дать прогноз среднего значения цены и доверительных интервалов для него.

Цена автомобиля зависит от множества факторов. К числу объясняющих переменных можно отнести, например, модель автомобиля, фирму-производитель, регион производства (Европа, США, Япония), объем двигателя, фирму-производитель, регион производства (Европа, США, Япония), объем производителя, количество цилиндров, время разгона до 100 км/час, пробег, потребление горючего, год выпуска и т.д. Первые из названных переменных очень важны при ценообразовании, но они – качественные. Традиционный регрессионный анализ, рассматриваемый в этом задании, предназначен для количественных данных. Поэтому, не претендуя на высокую точность, не будем включать их в эконометрическую модель. Сделаем выборку, например, только для автомобилей одной фирмы-производителя. Пусть, например, оказалось, что продано n= 16 таких автомобилей. Для упрощения выберем из базы данных цены y_i (i = 1......16) проданных автомобилей и только две объясняющие переменные: возраст х_{i 1} (i = 1, …..16) в годах и мощность двигателя х_{i 2} (i = 1, ….16) в лошадиных силах. Выборка представлена в таблице:

I номер	yi , цена, тыс. у.е.	хi1 возраст,лет	хi2 , мощность двигателя
1	11	5,0	155
2	6	7,0	87
3	9,8	5,0	106
4	11	4,0	89
5	12,3	4,0	133
6	8,7	6,0	94
7	9,3	5,0	124
8	10,6	5,0	105
9	11,8	4,0	120
10	10,6	4,0	107
11	5,2	7,0	53
12	8,2	5,0	80
13	6,5	6,0	67
14	5,7	7,0	73
15	7,9	6,0	100
16	10,5	4,0	118

1. Построить поля рассеяния между ценой y и возрастом автомобиля х₁ , между ценой y и мощностью автомобиля x₂ . На основе их визуального анализа выдвинуть гипотезу о виде статистической зависимости y от х₁ и y от х₂ . Найти точечные оценки независимых параметров

а₀ а₁ модели y = а₀ + а₁ х₁ + ε и

β₁ β₂ модели y = β₀ + а₁ х₁ + δ

2. Проанализировать тесноту линейной связи между ценой и возрастом автомобиля, а также ценой и мощностью двигателя х₂ . Для этого рассчитать коэффициенты парной корреляции r_{yx 1} и r_{yx 2} и проверить их отличие от нуля при уровне значимости α = 0,1.

3. Проверить качество оценивания моделей на основе коэффициента детерминации, F- и t- критериев при уровне значимости α = 0,05 и α = 0,10.

4. Проверить полученные результаты с помощью средств MicrocoftExcel.

5. С помощью уравнений регрессии рассчитать доверительные интервалы для среднего значения цены, соответствующие доверительной вероятности 0,9. Изобразить графически поля рассеяния, линии регрессии и доверительные полосы.

На продажу поступила очередная партия однотипных автомобилей. Их возраст х₁ равен 3 года. Мощность двигателя х₂ = 165 л.с. Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей по моделям y = а₀ + а₁ х₁ + ε и y = β₀ + а₁ х₁ + δ с доверительной вероятностью 0,9.

Решение:

На основе поля рассеяния, построенного на основе табл. 1, выдвигаем гипотезу о том, что зависимость цены y от возрастаавтомобиля x₁ описывается линейной моделью вида

y = а₀ + а₁ х₁ + ε

где а₀ и а₁ – неизвестные постоянные коэффициенты, а ε – случайная переменная (случайное возмущение), отражающая влияние неучтенных факторов и погрешностей измерений.

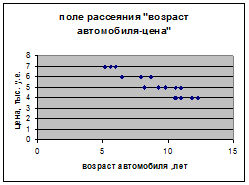
Рисунок 1 – Поле рассеяния «возраст автомобиля-цена»

Аналогично, на основе анализа поля рассеяния (рис. 2), также построенного на основе таблицы 1, выдвигаем гипотезу о том, что зависимость цены y от мощности автомобиля x₂ описывается линейной моделью вида

y = β₀ + β₁ х₁ + δ

где β₀ и β₁ – неизвестные постоянные коэффициенты, а ε – случайная переменная (случайное возмущение), отражающая влияние неучтенных факторов и погрешностей измерений.

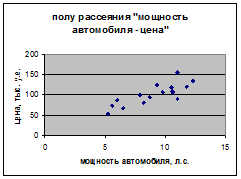
Рисунок 2 – Поле рассеяния «мощность автомобиля-цена»

На основе табл. 1 исходных данных для вычисления оценок параметров моделей составляется вспомогательная табл. 1.1. Воспользуемся формулами и левой частью таблицы 1.1. для нахождения оценок а₀ и а₁ .

Так как n = 16, получаем

= 145/16=9.0625

= 84.0/16=5.25

= 27.5625

= 365

= 460

i	yi	xi1	xi1 2	xi1 yi	yi 2	i	yi	xi2	xi2 2	xi2 yi
1	11	5.0	25	55	121	1	11	155	24025	1705
2	6	7.0	49	42	36	2	6	87	7569	522
3	9,8	5.0	25	49	96,04	3	9,8	106	11236	1038,8
4	11	4.0	16	44	121	4	11	89	7921	979
5	12,3	4.0	16	49,2	151,29	5	12,3	133	17689	1635,9
6	8,7	6.0	36	52,2	75,69	6	8,7	94	8836	817,8
7	9,3	5.0	25	46,5	86,49	7	9,3	124	15376	1153,2
8	10,6	5.0	25	53	112,36	8	10,6	105	11025	1113
9	11,8	4.0	16	47,2	139,24	9	11,8	120	14400	1416
10	10,6	4.0	16	42,4	112,36	10	10,6	107	11449	1134,2
11	5,2	7.0	49	36,4	27,04	11	5,2	53	2809	275,6
12	8,2	5.0	25	41	67,24	12	8,2	80	1600	656
13	6,5	6.0	36	39	42,25	13	6,5	67	4489	435,5
14	5,7	7.0	49	39,9	32,49	14	5,7	73	5329	416,1
15	7,9	6.0	36	47,4	62,41	15	7,9	100	10000	790
16	10,5	4.0	16	42	110,25	16	10,5	118	13924	1239
Сумма	145,1	84.0	460	726,2	1393,15	145,1	1611	167677	15327,1

Следовательно,

--> ЧИТАТЬ ПОЛНОСТЬЮ <--