Контрольная работа: Расчет индуктивности

Методы расчета индуктивностей

Индуктивностью (коэффициентом самоиндукции) называют коэффициент пропорциональности между током и возбуждаемым им потокосцеплением. Если речь идет об отношении потокосцепления одного из двух контуров в силе обусловливающего его тока в другом контуре, то говорят о взаимной индуктивности (коэффициенте взаимной индуктивности).

Поскольку индуктивность, как это следует из определения, зависит от распределения тока в проводниках, при ее расчете надо учитывать влияние частоты. Под низкой частотой понимается такая, при которой можно пренебречь неравномерностью распределения тока по сечениям проводов; длина электромагнитной волны при этом значительно больше линейных размеров сечения. Под весьма высокой частотой понимают частоту, длина волны которой значительно меньше размеров поперечного сечения провода; при этом ток можно считать сосредоточенным в поверхностном слое нулевой толщины. Высокие частоты занимают промежуточное положение.

С практической точки зрения целесообразно рассмотреть отдельно методы расчета индуктивности воздушных контуров, катушек с замкнутыми сердечниками и катушек с сердечниками, имеющими воздушный зазор.

Воздушные контуры

Под воздушными контурами подразумевают такую систему проводов, для которых магнитная проницаемость равна проницаемости окружающей среды. Расчет в общем случае сводится к следующему. Задаваясь токами в рассматриваемых контурах, разбивают каждый из токов на элементарные нити и на основе закона Био-Савара определяют индуктивность в выбранной точке поля. По ее значению находят поток, сцепляющийся с какой-нибудь нитью тока, затем вычисляют полный магнитный поток, сцепляющийся с рассматриваемым контуром и определяемый соответствующим током.

Если справедливо предположение, что ток распределен равномерно по сечению или по поверхности провода, применяют вариант метода, заключающийся в следующем. Поток, сцепляющийся с какой-нибудь нитью тока, выражают как сумму потоков взаимной индукции, создаваемых другими нитями, причем суммирование должно быть распространено на все нити данного контура при вычислении взаимной индуктивности. При этом получают выражения, содержащие в явном виде указания на необходимые математические операции.

Таким образом, имеем

;

;

,

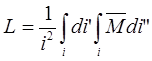где L и M – собственная и взаимная индуктивности; di – нити тока; dl – элементы длины нитей; Ө - угол между элементами; μ₀ – магнитная постоянная.

Сложность расчетов приводит к тому, что выше приведенным методом определяют индуктивность либо проводов простой формы, либо участков, составляющих сложные контуры. В последнем случае индуктивность контура состоит из суммы индуктивностей всех участков и двойной суммы взаимной индуктивности между участками, т.е.

(k ≠ i),

где n – число участков.

Получение расчетных соотношений для индуктивности возможно на основе и иных соображений. По определению индуктивность

,

где I – ток; Ψ – обусловленное им потокосцепление; ω – число витков; G – некоторая величина, являющаяся функцией геометрических размеров системы и имеющая размерность магнитной проводимости.

Если частные потоки сцепляются со всеми витками, то для расчета индуктивности берется проводимость пространства, в котором рассматривается суммарный поток.

Расчет индуктивностей катушек выполняют по одному из двух методов суммирования или массивного витка. Метод суммирования, заключающийся в учете частичных собственных и взаимных индуктивностей отдельных витков, не имеет явных преимуществ и применяется довольно редко (главным образом для численных расчетов катушек сложной формы). Методом массивного витка сравнивают индуктивность рассматриваемой катушки с индуктивностью массивного витка, имеющего такую же форму и размеры, при этом предполагая, что коэффициент заполнения равен единице. Таким образом, находят расчетную индуктивность, к которой затем вычисляют поправки на изоляцию.

Катушки с замкнутыми магнитопроводами (сердечниками). Расчет индуктивности катушек в магнитопроводах замкнутой формы осуществляют по общим соотношениям для магнитных цепей. В конечном своем виде эти соотношения отличаются от результатов, полученных для воздушных катушек, наличием множителя, учитывающего свойства сердечника и равного его магнитной проницаемости.

Для получения практических формул принимают, как правило, что весь магнитный поток проходит через магнитопровод (без утечек и рассеивания), а средняя магнитная силовая линия пронизывает центры масс поперечных сечений магнитной цепи (т. е. совпадает со средней линией магнитопровода). Исключением являются особые случаи, например катушки на сердечниках тороидальной формы с неполной обмоткой.

Если для какой - либо цепи возможно интегральное определение формализованной магнитной проводимости (или сопротивления), для вычисления индуктивности можно использовать формулу

,

связывающую индуктивность с магнитным сопротивлением R_M , в виде

,

где S_M - площадь поперечного сечения магнитопровода;l_M - длина средней магнитной силовой линии; μ_a - абсолютная магнитная проницаемость материала сердечника.

Катушки с сердечниками, имеющими воздушный зазор

Для магнитопроводов с большим воздушным зазором необходимо учитывать отклонение распределения поля в зазоре от идеализированного. При этом магнитные сопротивления для основного потока и потока рассеивания становятся соизмеримыми, и расчетные формулы существенно усложняются.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--