Контрольная работа: Расчет индуктивности
На практике удобно применять метод эквивалентного зазора, позволяющий использовать все формулы для сердечников с малыми зазорами. При этом эквивалентным зазором называют такой, который имеет ту же проводимость, что и реальный, а геометрия его определяется сечением полюсов магнитопровода и некоторой эквивалентной длиной. Эквивалентную длину находят из условия равенства проводимости на основе аппроксимации возможных путей потока.
Применительно к элементам радиоэлектронных цепей случай больших зазоров встречается сравнительно редко (исключение – катушки на стержневых сердечниках), и большая точность расчетов при этом не требуется. Индуктивность катушек на стержневых сердечниках определяют с помощью магнитной проницаемости тела (сердечника), выражаемой через коэффициент размагничивания. В этом случае коэффициент размагничивания равен проводимости (формально введенной) окружающего сердечник пространства при условии, что весь поток проходит через торцы сердечника.
Если известен для данного сердечника коэффициент размагничивания, то индуктивность катушки легко найти путем рассмотрения магнитной цепи, состоящей из двух участков с известными магнитными сопротивлениями.
В тех случаях, когда для расчетов используют коэффициент размагничивания, в формулы вместо μr подставляют μ0 (относительную магнитную проницаемость сердечника)
![]()
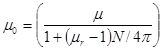 ,
,
где N – коэффициент размагничивания.
Основная сложность заключается в определении коэффициентов размагничивания, зависящих в общем случае от геометрических размеров сердечника, магнитных свойств материала сердечника и характера распределения намагничивающего поля катушки.
Индуктивность воздушных катушек и тел специальной формы
Рассмотрим формулы для расчета индуктивности элементов, для которых магнитная проницаемость равна проницаемости окружающего пространства. Под общим названием «тела специальной формы» объединены элементы, не являющиеся катушками в собственном смысле, но входящие в состав цепей РЭА (провода, электроды, кабели и т. д.). Предполагается, что проводники выполнены из немагнитного материала.
Все линейные размеры приведены в сантиметрах, индуктивность в микрогенри.
Однослойная воздушная катушка со сплошной намоткой.
![]() при
при ![]() <
< ![]() ,
,
где d – диаметр катушки; l – длина катушки; ω – число витков катушки;
![]() при
при ![]() > 5.
> 5.
Многослойная воздушная катушка:
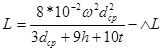 ;
;
где dср – средний диаметр катушки; h – высота катушки; t – радиальная ширина намотки; ∆ L – поправка на заполнение:
![]() ,
,
где dиз – диаметр провода в изоляции; dм – диаметр провода по меди.
Катушка со спиральной намоткой ленточным проводом.
Расчет индуктивности практически совпадает с расчетом L для многослойной катушки с теми же наружным и внутренним диаметрами, высотой и коэффициентом заполнения. Вместо числа витков в формулу подставляют число слоев ленточной катушки.
Соленоид на каркасе прямоугольного сечения:
![]() при
при ![]() ;
;
a, b – стороны поперечного сечения каркаса, a < b; l – длина катушки; k1 - на рис 1;
![]() при
при ![]() ;
;
где ![]() ;
; ![]() .
.
Значение поправок α1 и α2 приведены в таблице 1.
Табл. 1. Значения поправок α1 и α2 .
| a/b | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| α1 | 0,112 | 0,183 | 0,238 | 0,285 | 0,325 | 0,361 | 0,393 | 0,422 | 0,449 | 0,473 |
| α2 | 0,016 | 0,032 | 0,048 | 0,064 | 0,080 | 0,096 | 0,111 | 0,127 | 0,143 | 0,159 |
Погрешность расчетов индуктивности для l / b ≥ 1 определяют по рисунку 2, где ε – верхняя оценка относительной погрешности.