Контрольная работа: Решение математических уравнений и функций

Координаты точки Р найдем как решение системы:

, , .

Р(4;6).

5) Координаты основания медианы будут:

6)

, ,

М(3.5;2).

Уравнение медианы найдем, используя формулу , как уравнение прямой, проходящей через две точки: С и М.

, , ,

- уравнение медианы СМ.

7) Треугольник АВС задается пересечением трех полуплоскостей, определяемых через уравнения прямых АВ, ВС, АС.

Найдем уравнения ВС и АС по формуле .

, , ,

- уравнение ВС.

, , ,

- уравнение АС.

- уравнение АВ.

Чтобы определить полуплоскость, в которой лежит треугольник АВС относительно прямой АВ, подставим координаты точки С в уравнение АВ:

4∙8-3∙3-8=32-9-8=15≥0.

Тогда полуплоскость, в которой лежит треугольник АВС относительно прямой АВ, определяется неравенством: .

Аналогично для прямых ВС и АС.

; .

; .

Таким образом, треугольник АВС определяется системой неравенств:

.

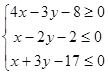Ответ003A

1) ;

2) ;

3) ; ;