Контрольная работа: Решение математических уравнений и функций

5) ;

6) .

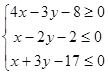Задание 2

Даны векторы . Доказать, что векторы образуют базис четырехмерного пространства, и найти координаты вектора в этом базисе.

Решение:

- система из четырех четырехмерных векторов. Следовательно, чтобы доказать, что она является базисом пространства , достаточно доказать ее линейную независимость.

Составим и вычислим определитель матрицы, столбцами которой являются векторы :

.

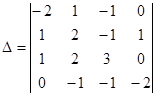Для вычисления этого определителя, разложим его по четвертому столбцу:

.

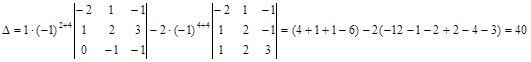Определитель Δ≠0, следовательно - линейно независимая система из четырех четырехмерных векторов, то есть базис пространства .

Для нахождения координат вектора в этом базисе, разложим вектор по базису :

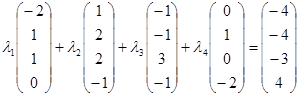.3

Найдем - координаты вектора в этом базисе.

.

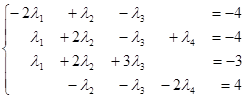Решим эту систему методом Гаусса.

Поменяем местами первое и третье уравнение:

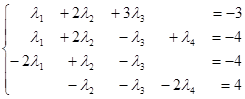
Первое уравнение, умноженное последовательно на (-1) и (2), прибавим соответственно ко второму и третьему уравнениям системы:

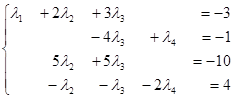
Поменяем местами второе и четвертое уравнения, третье разделим на 5:

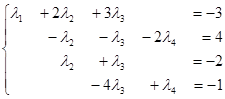
Прибавим к третьему уравнению второе:

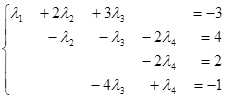
Поменяв местами третье и четвертое уравнение, получим систему треугольного вида:

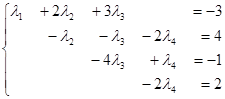
Система имеет единственное решение. Решаем снизу вверх:

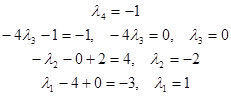
Вектор в базисе имеет координаты .