Контрольная работа: Решение практических заданий по дискретной математике
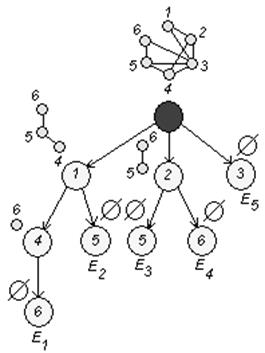
Построим таблицу:
1 2 3 4 5 6
1. {1,4,6} 1 1 1 
2. {1,5} 1 1
3. {2,5} 1 1
4. {2,6} 1 1
5. {3} 1
Определяем минимальное число строк, покрывающих все столбцы таблицы. Такими строками могут быть строки 1, 3, 5. Значит,
.
Зададимся красками: для множества вершин 
- краска синяя (С ), для множества вершин 
- краска красная ( К ), для множества вершин 
- краска зеленая ( З ).
Раскрасим вершины графа G :
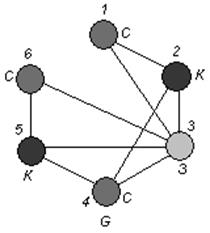
Задание 7
Для заданной сети 
:
а) найти величину минимального пути и сам путь от вершины 
до вершины 
по алгоритму Дейкстры ;
б) используя алгоритм Форда-Фалкерсона, определить максимальный поток 
( v1 – вход , v6 – выход сети ) и указать минимальный разрез, отделяющий v1 от v6 ,
если задана матрица весов (длин, пропускных способностей) Р :
v1 v2 v3 v4 v5 v6
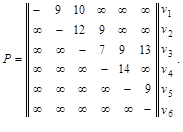
Решение:
Построим сеть:
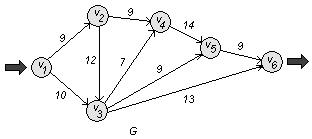
а) Найдем величину минимального пути и сам путь сети G . Используем для этого алгоритм Дейкстры.
Этап 1. Нахождение длины кратчайшего пути.
.
Шаг 1. Полагаем 
1-я итерация.