Контрольная работа: Решение практических заданий по дискретной математике
Так как все импликанты участвовали в склеивании, и сокращенная ДНФ состоит из одной простой импликанты, то строить таблицу покрытий нет необходимости, т.е.
.
Задание 6
Для неориентированного графа 
, у которого 
, 
а) вычислить числа 
;
б) определить хроматическое число 
.
Решение:
Построим граф:
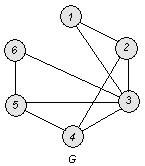
а) Вычислим числа 
.
1) 
:
Используя алгоритм выделения пустых подграфов, построим дерево:
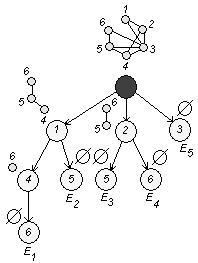
Согласно определению :
.
2) 
:
Используя алгоритм выделения полных подграфов, построим дерево:
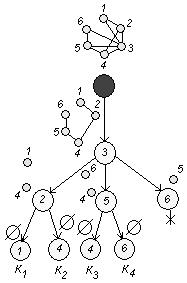
Здесь 
- полные подграфы. Видно, что мощность носителей всех подграфов равна трем, т.е.
.
3) 
:
Построим модифицированную матрицу смежности 
заданного графа G :
1 2 3 4 5 6
.
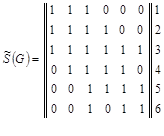
Находим минимальное число строк, покрывающих все столбцы модифи-цированной матрицы . Таких строк – одна. Следовательно,
.
б) Определим хроматическое число 
.