Контрольная работа: Решение практических заданий по дискретной математике
8. Используя алгоритм Краскала, построить остов с наименьшим весом для неориентированного взвешенного графа ![]() , у которого
, у которого ![]() , если заданы веса (длины) ребер:
, если заданы веса (длины) ребер:
![]()
□ Построим граф G :
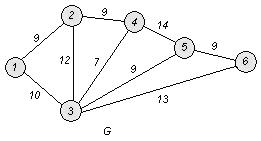
1. Упорядочим ребра в порядке неубывания веса (длины):
![]()
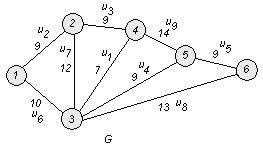
2. Возьмем ребро u1 и поместим его в строящийся остов.
Возьмем ребро u2 и поместим его в строящийся остов (т.к. оно не образует с предыдущим ребром цикла).
Берем ребро u3 и помещаем его в строящийся остов (т.к. оно не образует с предыдущими ребрами цикла).
Берем ребро u4 и помещаем его в строящийся остов (т.к. оно не образует с предыдущими ребрами цикла).
Берем ребро u5 и помещаем его в строящийся остов (т.к. оно не образует цикла с предыдущими ребрами).
Ребра ![]() не рассматриваем, т.к. они образуют циклы с предыдущими ребрами.
не рассматриваем, т.к. они образуют циклы с предыдущими ребрами.
Проверим окончание алгоритма. Число входящих в остов ребер равно 5. Заданный граф имеет п = 6 вершин и ![]() . Таким образом, остов содержит все вершины заданного графа G .
. Таким образом, остов содержит все вершины заданного графа G .
Вес (длина) построенного остова
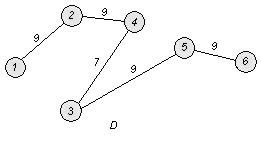
равен ![]()
![]() .
.
Литература
1. Горбатов В.А. Основы дискретной математики. – М.: Высшая школа, 1986. – 311 с.
2. Коршунов Ю.М. Математические основы кибернетики. – М.: Энерго атомиздат, 1987. – 496 с.
3. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988. – 480 с.
4. Шапорев С.Д. Дискретная математика. – СПб.: БХВ-Петербург, 2006. - 400 с.
5. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике. – М.: ФИЗМАТЛИТ, 2005. – 416 с.
6. Хаханов В.И., Чумаченко С.В. Дискретная математика ( конспект теоретического материала). – Харьков: ХНУРЭ, 2003. – 246 с.
7. Богданов А.Е. Курс лекций по дискретной математике.–Северодонецк: СТИ, 2006. – 190 с.