Контрольная работа: Системи лінійних рівнянь

Постановка задачі. Потрібно знайти значення х 1, х 2, … , хn , що задовольняють таким співвідношенням: .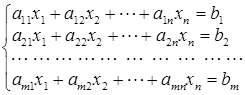

Тут aij (i = 1, 2, … , m ; j = 1, 2, … , n ) і bk (k = 1, 2, … , m ) – задані числа.

При цьому:; ; .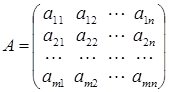

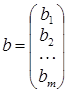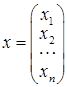Матриця А називається головною матрицею системи, вектор b – вектором-стовпцем правих частин, вектор x – вектором-стовпцем невідомих.

Використовуючи ці позначки, можна систему записати в матричній формі: Ах = b .

Якщо b 1 = b 2 = ¼ = bm = 0, то система рівнянь називається однорідною . Якщо хоча б одне з bk (k = 1, 2, ¼ , m ) відмінне від нуля, то система називається неоднорідною .

.

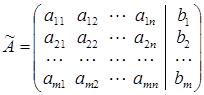Матриця називається розширеною матрицею системи.

Якщо система має хоча б один розв’язок, то вона називається сумісною .

При цьому система, що має єдиний розв’язок, називається визначеною , а більше одного розв’язку – невизначеною .

Якщо система не має розв’язків, то вона називається несумісною .

При розв’язуванні систем лінійних рівнянь має бути знайдена відповідь на три запитання:

А. Чи сумісна система?

В. Чи визначена система?

С. Як знайти розв’язок (чи розв’язки) системи, якщо вони існують?

Правило Крамера. Якщо неоднорідна система рівнянь невироджена (detА ¹ 0), то система визначена, тобто має єдиний розв’язок, і його можна знайти за формулами Крамера: (k = 1, 2, … , n ) де Dk – визначник матриці, яку можна одержати, якщо в матриці А системи k- й стовпець замінити на стовпець вільних членів.

Ранг матриці. З розв’язуванням систем рівнянь безпосередньо пов'язане поняття рангу матриці. Ранг матриці – це найвищий порядок її мінора, відмінного від нуля.

Для того щоб знайти ранг матриці, важливо орієнтуватися в тому, які перетворення з матрицею можна робити, не змінюючи при цьому її ранг:

1) транспонування;

2) перестановка двох рядків (стовпців);

3) множення всіх елементів рядка (або стовпця) на число a¹ 0;

4) додавання до всіх елементів рядка (стовпця) відповіднихелементів іншого рядка (стовпця);

5) вилучення нульового рядка (стовпця);

6) викреслення рядка (стовпця), що є лінійною комбінацією інших рядків (стовпців).

Однорідні системи. Розглядається однорідна система лінійних рівнянь з n невідомими: Ах = 0.

Якщо rangА = n (detА ¹ 0), то система визначена і має тільки тривіальний розв’язок: x 1 = x 2 = … = xn = 0.

Якщо rangА < n (detА = 0), то система має не тільки тривіальні розв’язки. При цьому всі розв’язки однорідної системи рівнянь утворюють лінійний простір L і dim L = n – rangА .

Щоб знайти базис простору розв’язків однорідної системи рівнянь, треба:

1.Знайти базисний мінор матриці А .

--> ЧИТАТЬ ПОЛНОСТЬЮ <--