Контрольная работа: Системи лінійних рівнянь

Звідси укладаємо, що .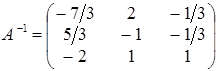

Задача 4. Знайти матрицю, яка є оберненою до .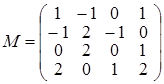

Розв’язання. Для обернення матриці застосуємо першу формулу Фробеніуса. Позначимо: , , , .

Знаходимо послідовно:

;

;

;

.

І тоді 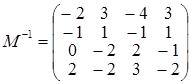. Привабливість зазначеного способу полягає в тому, що для обернення матриці 4-го порядку ми маємо справу з оберненням матриць лише 2-го порядку, що істотно простіше.

Задача 5. За допомогою правила Крамера розв’язати систему лінійних неоднорідних рівнянь: .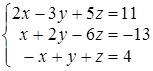

Розв’язання. Головна матриця системи має вигляд: .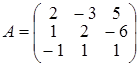

Розв’язок системи може бути знайдений за правилом Крамера, тому що detА = D = 18 ¹ 0. Для цього побудуємо визначники Dх , Dу , Dz , які відрізняються від головного визначника тим, що в ньому стовпець коефіцієнтів при, відповідно, х , у та z замінено на стовпець вільних членів, тобто:

.

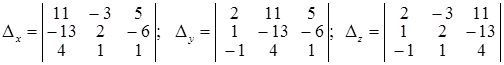Обчислюючи їх, знаходимо, що Dх = 18, Dу = 36, Dz = 54.

Отже .

Задача 6. Розв’язати систему лінійних однорідних рівнянь:

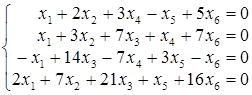
Розв’язання. Насамперед відзначимо, що система напевне сумісна, оскільки однорідна система завжди має щонайменше нульовий розв’язок.

Почнемо пошук загального розв’язку даної системи. Головна матриця системи має вигляд: .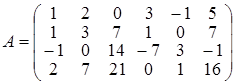

Знайдемо ранг матриці А. Перший рядок матриці з відповідними множниками додамо до інших рядків матриці так, щоб елементи першого стовпця обернулися на нуль, крім елемента а 11. Вийде матриця А 1 така, що

rangА 1 = rangА і .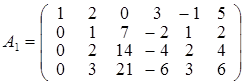

Відзначаючи, що третій і четвертий рядки матриці пропорційні другому рядку, укладаємо, що rangА 1 = rangА 2, де . Помножимо другий рядок матриці А 2 на (–2) і додамо до першого рядка. Одержимо матрицю А3: , таку, що rangА 3 = rangА 2 = 2. У підсумку rangА = rangА 3 = 2.

Тоді вийшла система двох рівнянь, з яких можна написати:

х 1 = 14х 3 – 7х 4 + 3х 5 – х 6, х 2 = –7х 3 + 2х 4 – х 5 – 2х 6 і змінні х 3, х 4, х 5, х 6 – будь-які. Це і є розв’язок системи.

Однак можна (і необхідно) піти далі. Множина розв’язків лінійної однорідної системи утворює лінійний простір L вимірності dimL = n – rangА = 6 – 2 = 4. Для знаходження базисних векторів простору розв’язків надамо вільним невідомим х 3, х 4, х 5, х 6 значення: а) 1, 0, 0, 0; б) 0, 1, 0, 0; в) 0, 0, 1, 0; г) 0, 0, 0, 1. Одержимо чотири вектори, що утворять базис L : е 1 = (14, –7, 1, 0, 0, 0); е 2 = (–7, 2, 0, 1, 0, 0); е 3 = (3, –1, 0, 0, 1, 0); е 4 = (–1, –2, 0, 0, 0, 1). У такий спосіб L = ℒ(е 1, е 2, е 3, е 4), і будь-який розв’язок вихідної системи може бути записаний у вигляді лінійної комбінації базисних векторів, тобто у вигляді: с 1(14, –7, 1, 0, 0, 0) + с 2(–7, 2, 0, 1, 0, 0) + с 3(3, –1, 0, 0, 1, 0) + с 4(–1, –2, 0, 0, 0, 1), де с 1, с 2, с 3, с 4 – будь-які значення. Це і є загальний розв’язок вихідної лінійної однорідної системи рівнянь.

Задача 7. Розв’язати систему лінійних неоднорідних рівнянь

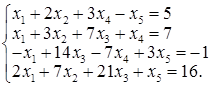
Розв’язання. Розширена матриця системи рівнянь має вигляд: , причому до вертикальної риски записана головна матриця системи, а після вертикальної риски – стовпець вільних членів. Перетворюючи матрицю аналогічно до того, як перетворювалася матриця А в розв’язку попередньої задачі, одержимо матрицю А таку, що rang = rangА = 2 і . Звідси можна записати загальний розв’язок системи у вигляді: х 1 = 1 + 14х 3 – 7х 4 – 3х 5, х 2 = 2 – 7х 3 + 2х 4 – х 5, де х 3, х 4, х 5 – будь-які.

Це і є загальний розв’язок вихідної системи лінійних рівнянь. Однак з метою прояснення алгебраїчної структури розв’язку системи відзначимо таке: