Контрольная работа: Системи лінійних рівнянь

4. Чому дорівнює вимірність простору розв’язків однорідної системи лінійних рівнянь, якщо в системі 10 рівнянь, 16 невідомих і ранг матриці системи дорівнює 6?

5. Чи утворює множина розв’язків неоднорідної системи лінійний простір? Яка з властивостей лінійного простору не виконується?

6. Згадайте визначення лінійного многовиду. Що називається його базисом і вимірністю?

7. Як визначається вектор зсуву для лінійного многовиду, що є множиною розв’язків неоднорідної системи?

3. Приклади розв’язування задач

Задача 1. Знайти ранг матриці .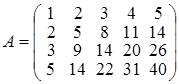

Розв’язання. Насамперед відзначимо, що четвертий рядок матриці є сумою другого і третього рядків і тому при вилученні цього рядка ранг матриці не зміниться.

1.Відкинемо четвертий рядок.

2.З другого і третього рядків матриці віднімемо перший рядок, помножений, відповідно, на 2 та 3.

3.В отриманій матриці з третього рядка віднімемо другий, помножений на 2.

Одержимо ланцюжок перетворень:

лінійний рівняння матриця

.

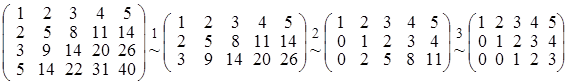У матриці, що утворилась, мінор, який стоїть в перших трьох стовпцях, не дорівнює нулю. Отже, ранг вихідної матриці дорівнює 3 і мінор 3-го порядку, що стоїть в перших трьох стовпцях, є базисним мінором матриці А.

Задача 2. Знайти матрицю, яка є оберненою до матриці

.

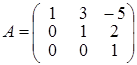Розв’язання. Знайдемо обернену матрицю за визначенням. Нехай обернена матриця має вигляд: 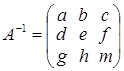. Тоді, за визначенням,

АА –1 = Е , тобто .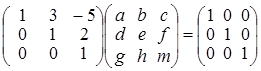

Знаходячи добуток матриць, одержимо рівності:

.

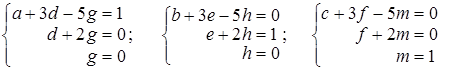Із цих співвідношень одержуємо: g = 0, d = 0, a = 1; далі: h = 0, e =1, b = –3. І нарешті: m = 1, f = –2, c = 11. У підсумку дійдемо висновку, що:

.

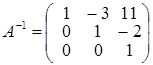Задача 3. Знайти матрицю, яка є оберненою до матриці .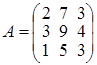

Розв’язання. Побудуємо матрицю 6 ´ 6, дописавши праворуч від А одиничну матрицю Е , внизу матрицю (– Е ), а інші місця заповнимо нулями.

.

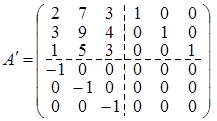За допомогою операцій над рядками матриці А ¢ утворимо на місці (–Е ) нульову матрицю. Тоді в правому нижньому куті буде стояти матриця А –1.

1.До всіх рядків матриці А ¢ додамо третій рядок з деяким множником, домагаючись того, щоб всі елементи першого стовпця, крім а 31, дорівнювали нулю.

2.Перший рядок отриманої матриці поділимо на (–3) і, додаючи до інших рядків матриці отриманий перший рядок з деякими множниками, досягаємо того, щоб у другому стовпці стояли нулі, крім елемента а 12.

3.За допомогою другого рядка утворимо нулі в третьому стовпці, крім елемента а 23.

Одержимо ланцюжок перетворень: