Контрольная работа: Техническая механика. Задачи

а b c a

9.6

3.8

+

+ 1

+

0.8

-

Задача №4 Изгиб

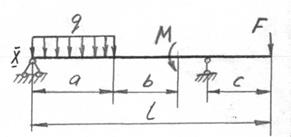
Для заданной схемы балки требуется написать выражение для определения изгибающего момента для каждого участка в общем виде, построить эпюру М, найти М_мах и подобрать стальную балку двутаврового поперечного сечения при [σ]= 160 МПа.

Таблица 5 – Исходные данные

а, м	b, м	с, м	l, м	М, кН·м	F, кН	q, кН/м
2.6	4.6	2.7	11	10	10	15

Уравнение прочности при изгибе в общем виде:

σ _и =

1.Составляем расчётную схему и методами теоретической механики определяем реакции в опорах. Предварительно определяем размер d:

d=l-(a+b+c) =11- (2.6+4.6+2.7) =1.1 м

ΣМ_А = 0 , - (2q·а) · ( - P·d +R_B · (d+b) +M = 0

R_B =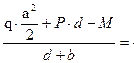

15·3.38+10·1.1-10

R_B =————————— = 29.52

1.1+4.6

ΣМ_B =0

- (2q·а)·(b+d+()-R_А (d+b)+P·b+М=0

R_А =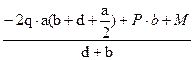

-30·(4.6+1.1+1.3)+10·4.6+10

R_А = ——————————————— = -27.01

1.1.+4.6

т.е. реакция направлена в другую сторону, чем на схеме.

2.Определяем изгибающие моменты, действующие по длине балки, используя правило знаков для изгибающего момента.

Изгибающий момент на участке с координатой Х₁ :

М_И1 =2q·Х₁ ·

при Х₁ =0,М_И =0

при Х₁ =а, М_И = 30·6.76/2 = 101.4

(кривая на эпюре парабола, т.к. переменная Х₁ во второй степени).

Изгибающий момент на участке с координатой Х₂ :

М_ИII = 2q·а ·(Х₂ -+R_A ·(Х₂ -а)

при Х₂ =а, М_И =2q·а· (+R_А ·(а-а)=101.4 кН·м