Контрольная работа: Уравнение равновесия. Проекция скорости точки

S=10·10+ (10·10+0,5·10·20) +10·30+0,5·10·30=750 v

В данном случае максимальное расстояние от исходного положения составит 750 м, точка в конце движения будет находится также на расстоянии 750 м.

Задача 8.3 В механизме качающегося грохота (рис.8.3) определить угловую скорость кривошипа О₂ В=3r и скорость ползуна D при вертикальном положении кривошипа O₁ A, если АВ=CD=2r. Отношение BC/CO₂ =3/5, угловая скорость кривошипа О₁ А равна ω=6 рад/с, углы α=60º, β=45º. Длина кривошипа O₁ A равна r=0.1м.

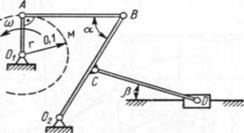
Дано:

O₁ A=r=0,1 м

AB=CD=2r=0,2 м

O₂ B=3r=0,3 м

ω_{OA 1} =6 рад/с

α=60º

β=45º

ω_O2B , V_D - ?

Построим положение механизма в соответствии с данными условиями задачи.

Для определения необходимых нам скоростей необходимо провести ряд промежуточных вычислений.

Определим скорость V_A

V_A =ω_O1A ·r/2=6·0,1=0,6м. с (V_A ┴O₁ A)

Скорость V_A определяем с помощью теоремы о проекциях скоростей двух точек тела (стержня АВ) на прямую соединяющую эти точки (прямая АВ).

V_A =V_B cos30 → V_B =0.6/cos30=0,69м/c²

Построим мгновенный центр скоростей (МЦС) - точка лежащая на пересечении перпендикуляров к векторам V_A и V_B

ω_{O 2 B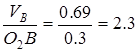} = рад/с

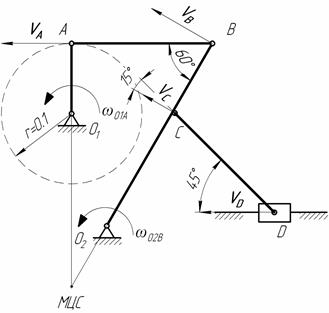
Определяем V_D . Точка D принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно и стержню CD. Поэтому чтобы найти ее скорость достаточно знать скорость какой-нибудь другой точки этого стержня и направление V_D .

Величину V_C найдем из пропорции

V_C = (V_C ┴СМЦС)

Скорость V_D определяем с помощью теоремы о проекциях скоростей двух точек тела (стержня CD) на прямую соединяющую эти точки (прямая CD).

V_D cos45=V_C cos15 → V_D =0,5·cos15/cos45=0,68 м/c²

Ответ: ω_{O 2 B} = рад/с; V_D =0,68 м/c²

Задача 3