Контрольная работа: Уравнения, содержащие параметр

2) получится условие, лишенное смысла.

В первом случае значение параметра считается допустимым, во втором – недопустимым.

Решить уравнение (неравенство), содержащее параметр, - это значит, для каждого допустимого значения параметра найти множество всех значений данного уравнения (неравенства).

К сожалению, не редко при решении примеров с параметрами многие ограничиваются тем, что составляют формулы, выражающие значения неизвестных через параметры. Например, при решении уравнения переходят к у равнению ; при m=записывают единственное решение 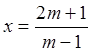. Но ведь при m= -1 – бесчисленное множество решений, а при m=1, решений нет.

Пример 1. Решить уравнение .

Сразу видно, что при решении этого уравнения стоит рассмотреть следующие случаи:

1) a=1, тогда уравнение принимает вид и не имеет решений;

2) при а=-1 получаем и, очевидно, х любое;

3) при .

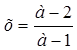Ответ: при a=1 решений нет, при а=-1 х любое, при .

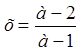Пример 2. Решить уравнение

Очевидно, что , а , то есть х=b/2, но , то есть 2b/2, b4.

Ответ: при b4 х=b/2; при b=4 нет решений.

Пример 3. При каких а уравнение имеет единственное решение?

Сразу хочу обратить внимание на распространенную ошибку – считать данное уравнение квадратным. На самом деле это уравнение степени не выше второй! При а – 2=0, а = 2, уравнение вырождается в линейное имеет единственный корень х=1/4. Если же а2, то мы действительно имеем дело с квадратным уравнением, которое даёт единственное решение при D=0 , , а=1, а=6.

Ответ: при а=2, а=1, а=6.

1.1 Решение уравнений первой степени с одним неизвестным

Решить такое уравнение – это значит:

1) определить множество допустимых значений неизвестного и параметров;

2) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнений.

Простейшее уравнение первой степени с одним неизвестным имеет вид ах-b=0.

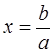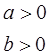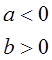При уравнение имеет единственное решение , которое будет: положительным, если или ; нулевым, если ; отрицательным, если или .

Если а=0, то при b=0 бесчисленное множество решений, а при b0 решений нет.

Пример 1. Для каждого значения а решить уравнение ; найти при каких а корни больше нуля.

Это уравнение не является линейным уравнением (т.е. представляет собой дробь), но при х-1 и х0 сводится к таковому: или а-1-х=0.

Мы уже выявили допустимые значения икс (х-1 и х0), выявим теперь допустимые значения параметра а:

а-1-х=0 а=х+1

Из этого видно, что при х0 а1, а при х-1 а0.

Таким образом, при а1 и а0 х=а-1 и это корень больше нуля при а>1.