Курсовая работа: Аналитический метод в решении планиметрических задач

Векторы а(а) и в(а) коллинеарны тогда и только тогда, когда их координаты пропорциональны.

Каждой точке М плоскости поставим в соответствие вектор ОМ(а) . Координаты вектора ОМ(а) называются координатами точки М в данной аффинной системе координат. При этом если ОМ(а) = (х, у) , то пишут: М (х, у).

Пусть прямые, проведенные через точку М параллельно осям координат, пересекают оси координат соответственно в точках М₁ и М₂ (рис. 2). Тогда имеем

ОМ(а) = ОМ(а)₁ + ОМ(а)₂ .

С другой стороны,

ОМ(а) = хе(а)₁ + уе(а)₂ .

Следовательно,

х =ОМ(а)₁ / е(а), у = ОМ(а)₂ / е(а)₂ .

Точки Е₁ и Е₂ имеют координаты: Е₁ (1; 0), Е₂ (0;1).

Если на плоскости даны две точки А (х₁ , у₁ ) и В (х₂ , у₂ ) , то координаты вектора АВ(а) вычисляются так:

АВ(а) = ОВ(а) - ОА(а) = (х₂ - х₁ , у₂ - у₁ ).

Пусть точка С делит отрезок АВ в данном отношении:

Тогда . Из правил действии над векторами в координатах следует, что координаты точки С определяются формулами:

,

В частности, если С – середина отрезка АВ , то

,

Рассмотрим различные способы задания прямой на плоскости.

Пусть требуется написать уравнение прямой l , заданной в некоторой аффинной системе координат точкой М₁ (х₁ , у₁ ) и ненулевым вектором , параллельным прямой l (рис. 3).

Вектор а(а) будет называться направляющим вектором прямой l .

Пусть М (х, у) – произвольная точка прямой l . Тогда, согласно условию, векторы и а(а) коллинеарны тогда и только тогда, когда выполняется равенство , или

ОМ(а) = ОМ(а)₁ + tа(а),

где t – некоторое число (параметр). Это соотношение в координатах запишется так:

Полученные уравнения называют параметрическими уравнениями прямой.

При и эти уравнения равносильны следующему уравнению первой степени:

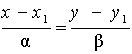
Если прямая задана двумя различными точками: А (х₁ , у₁ ) и В (х₂ , у₂ ), то вектор АВ(а) = (х₂ - х₁ , у₂ - у₁ ) является направляющим вектором прямой l . Следовательно, при х₁ х₂ и у₁ у₂ получаем уравнение

,

которое называется уравнением прямой, проходящей через две точки.