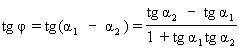Курсовая работа: Аналитический метод в решении планиметрических задач

Это уравнение называется уравнением прямой в отрезках.

Исключая из параметрических уравнений прямой параметр t . При получим уравнение:

у - у₁ = k (х - х₁ ),

где . Число k называют угловым коэффициентом прямой. В частном случае, при х₁ = 0 и у₁ = b , уравнение принимает вид

Если же , то прямая l параллельна оси О y , а её уравнение запишется так:

х = х₁ .

Таким образом, всякую прямую на плоскости можно задать уравнение первой степени Ах + Ву + С = 0 , где хотя бы одно из чисел А и В отлично от нуля. Верно и обратное предложение: всякое уравнение первой степени Ах + Ву + С = 0 есть уравнение некоторой прямой в аффинной системе координат на плоскости.

При уравнение Ах + Ву + С = 0 приводится к виду у = k х + b , где

,

Если же В = 0 и , то оно принимает вид х = а , где .

1.5. Декартова система координат на плоскости. Прямая и окружность.

Определение. Декартовой (или ортонормированной, или прямоугольной ) системой координат на плоскости называется такая аффинная система координат, базисные векторы которой ортонормированны, то есть имеют единичные длины и ортогональны (перпендикулярны). Обозначение R = { O , i(а) , j(а) }; так что | i(а) | = | j(а) | = 1 , i(а) перпендикулярен j(а) .

При решении задач, в которых существенную роль играет понятие расстояния между двумя точками, применяется, декартова или прямоугольная система координат.

Пусть даны две точки: А (х₁ , у₁ ) и В (х₂ , у₂ ). Тогда, как известно,

.

Пользуясь формулой, запишем уравнение окружности с центром в точке С ( a , b ) и радиусом r :

.

Вышеизложенная теория прямой справедлива и для прямоугольной системы координат. В частности, при решении задач пользуются уравнением прямой с угловым коэффициентом k , проходящей через точку А (х₁ , у₁ ):

.

Отсюда следует, что угловой коэффициент прямой, заданной двумя точками А (х₁ , у₁ ) и В (х₂ , у₂ ), вычисляется по формуле

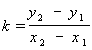
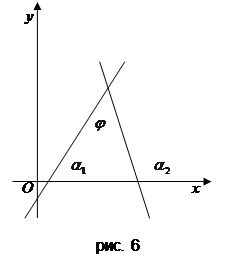Угловой коэффициент в прямоугольной системе координат имеет следующий геометрический смысл: , где – величина угла от оси абсцисс до прямой l .

Пусть прямые l ₁ и l ₂ заданы своими уравнениями с угловыми коэффициентами: у = k ₁ х + b ₁ и у = k ₂ х + b ₂ .

Если l ₁ || l ₂ , то , поэтому k ₁ = k ₂ , и обратно, т.е. условие k ₁ = k ₂ выражает признак параллельности прямых l ₁ и l ₂ .

Введем формулу для вычисления угла между пересекающимися прямыми l ₁ и l ₂ (рис. 6).

Так как и , , то