Курсовая работа: Аналитический метод в решении планиметрических задач

L ={М (х, у): F (х, у) = 0}.

Здесь необходимо отметить, что сформулированное определение линии оказывается весьма широким, так что под него попадают объекты, никак не отвечающие нашему наглядному (интуитивному) представлению о линии. Другими словами, далеко не каждое уравнение вида F (х, у) = 0 определяет на координатной плоскости геометрическую фигуру, которую мы склонны считать линией.

В качестве примера приведем два уравнения. Первое х - |х| = 0 , как легко видеть, определяет на координатной плоскости правую полуплоскость, так как оно равносильно неравенству: . Второе х+у-|х|-|у|=0 равносильно системе (конъюнкции) двух неравенств и потому определяет на плоскости одну точку, а уравнение х² + у² + 1 = 0 вообще не определяет на плоскости никакой геометрической фигуры.

Для того чтобы уравнение вида F (х, у) = 0 определяло геометрическую фигуру, отвечающую нашему наглядному представлению о линии, следует, вообще говоря, функцию F (х, у) = 0 подчинить некоторым ограничениям. Одним из таких является требование того, чтобы уравнение F (х, у) = 0 и у = f (х) были эквивалентны, т.е. любая пара действительных чисел, удовлетворяющая первому уравнению, удовлетворяет и второму, и наоборот. В этом случае, как нетрудно понять, линия L , определяемая уравнением F (х, у) = 0 , будет графиком функции f(х).

Таким образом, мы приходим еще к одному способу аналитического задания линий плоскости. Он называется явным: здесь линия задается уравнением у = f (х) , в котором у явно выражена через х , Этот способ хорошо известен из школьного курса алгебры и начала анализа. В отличие от него предыдущий способ, т.е. задание линии уравнением F (х, у) = 0 , называется неявным: здесь ни одно из неизвестных не выражено явно через другое.

Наконец, рассмотрим еще один способ задания линий – параметрический. При таком задании каждое из неизвестных х и у выражается как функция через третью, неизвестную, переменную t , называемую параметром:

L :

При каждом значении t Î D из некоторой области допустимых значений получаем значения х и у , которые представляют собой координаты некоторой точки линии: М (х. у) Î L .

Для примера получим параметрические уравнения окружности с центром в начале координат радиуса r . В качестве параметра выберем центральный угол t , который образует радиус-вектор ОМ(а) текущей точки М(х, у) с положительным направлением оси Ох (т.е. с вектором i(а) ). Тогда для того, чтобы точка М (х, у) обежало всю рассматриваемую окружность, нужно, чтобы угол t изменялся в пределах: t Î [0, 2p). Из r ONM находим:

х = ON = ОМ Ÿ со s t = r Ÿ cos t , у = MN = ОМ Ÿ sin t = r Ÿ sin t.

Эти формулы будут справедливы и для II – IV четвертей. Таким образом, мы приходим к параметрическим уравнениям окружности:

Из этих равенств можно исключить параметр t . Для этого нужно каждое из них возвести в квадрат и результаты сложить почленно. Получим:

х ² + у ² = r² cos² t + r² sin² t, x² + y² = r² (cos² t + sin² t), x² + y² = r² .

Мы приходим к знакомому нам уравнению.

Рассмотрим примеры задач на определение вида геометрической фигуры по её аналитическому заданию и их решения. В качестве аналитических условий, задающих геометрические фигуры, будем брать уравнения.

Пример. Исследовать геометрическую фигуру, задаваемую в аффинной системе координат уравнением: х – у = 0 . Представим данное уравнение в виде: . тогда ясно, что ему удовлетворяют координаты тех и только тех точек плоскости, радиус-векторы r(а) (х, у) которых коллинеарны вектору а(а) (1, 1) .

Отсюда следует, что рассматриваемая фигура есть прямая l , проходящая через начало координат и параллельная вектору а(а) (1, 1) . В случае, когда система координат декартова, прямая l есть биссектриса I и III координатных углов.

1.7. АЛГЕБРАИЧЕСКИЕ ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ

В этом разделе изучаются линии второго порядка, задаваемые в некоторой аффинной системе координат на плоскости алгебраическими уравнениями второй степени. Одна такая линия нам уже известна: это – окружность. Мы начнем с рассмотрения дальнейших конкретных примеров таких линий -эллипса, гиперболы и параболы.

Эти замечательные кривые были известны ещё древнегреческим математикам, начиная с IV в. до н.э. в связи со знаменитой задачей об удвоении куба, которую можно рассматривать как задачу о нахождении точки пересечения двух парабол х ² = у и у ² = 2х. В частности, Аристей в работе «О пространственных местах» уже рассматривал три различных типа конических сечений: эллипс, гиперболу и параболу. Основополагающий вклад в изучение этих линий внес Апполоний из Перги (около 260 – 177 гг. до н.э.). Его знаменитый трактат из восьми книг «О конических сечениях», из которого до нас дошли семь (известна реконструкция восьмой книги, предложенная современником И. Ньютона знаменитым астрономом Э. Галлеем) по своей фундаментальности сопоставим разве что с трактатом Евклида «Начала», написанном в III в. до н.э. Он установил многие важные свойства этих кривых, в частности, как канонических сечений, дал им современные названия «эллипс» - недостаток, «гипербола» - избыток (по отношению к некоторым свойствам параболы). Эта работа Аполлония по существу явилась идейным истоком аналитической геометрии. Декарт, когда в своей книге «Геометрия» (1637 г.) он использовал систему алгебраических обозначений, пришедшую с арабского востока (и которой мы пользуемся до сих пор!). Идею использовать алгебру при изучении геометрических фигур высказывал также другой современник Декарта Пьер Ферма. Именно он впервые установил, что уравнения первой степени задают прямые, а второй – конические сечения.

Определение. Эллипсом называется совокупность всех точек плоскости, сумма расстояний которых до двух данных точек этой плоскости (называемых фокусами эллипса), есть величина постоянная.

Пусть F ₁ , F ₂ –данные точки и расстояние между ними . Введем на плоскости декартову систему координат, приняв за ось Ох прямую (F ₁ F ₂ ), а за ось Оу – прямую, проходящую через середину О отрезка перпендикулярно оси Ох . Назовем эту систему координат канонической для рассматриваемого эллипса.

Теорема. В канонической системе координат уравнение Эллиса может быть записано в виде (оно называется каноническим уравнением эллипса):

. (1)

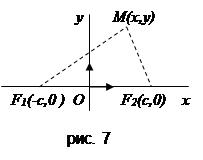Доказательство. В канонической системе координат имеем F ₁ (-с, 0), F₂ (с, 0). Для составления уравнения эллипса возьмем на нем произвольную (текущую) точку М (х, у) и найдем условия её принадлежности к рассматриваемому эллипсу . По определению имеем:

.