Курсовая работа: Анализ частотных свойств линейных избирательных цепей

Содержание

Введение

1. Нахождение спектральной плотности одиночного видео- и радиоимпульса

2. Расчет АЧС и ФЧС периодических видеоимпульсов

3. Расчет радиосигнала с амплитудной модуляцией на входе цепи

4. Расчет комплексного коэффициента передачи избирательной цепи

5. Расчет выходного сигнала при несовпадении несущей резонансной частот

6. Расчет выходного сигнала при совпадении несущей и резонансной частот

7. Расчет зависимости коэффициента демодуляции от модулируемой частоты

8. Отклик цепи при воздействии одиночного радиоимпульса

9. Прохождение частотно-модулированного колебания через избирательную цепь

Выводы

Перечень источников

радиоимпульс сигнал частота резонансная

Введение

Расчет отклика избирательной цепи на различные виды входного сигнала является одной из самых первых задач радиотехники. Ведь вся радиотехника начиналась с простейших радиопередатчиков и радиоприемников, но уже в них главным элементом была избирательная цепь. Избирательные цепи являются основным элементом любого радиоприемника. Основной задачей избирательной цепи на входе радиоприемника является выделение из всего спектра радиоволн необходимого сигнала. Кроме того, избирательные цепи в различных видах присутствуют во многих видах современной радиоаппаратуры.

На сегодняшний день основными в радиовещании являются два типа модуляции – амплитудная и фазовая. В данной курсовой работе рассмотрено прохождение основных видов сигналов с модуляцией радиочастоты полезным информационным сигналом через избирательную цепь. Также показано как изменяется спектр выходного сигнала при незначительной расстройке колебательного контура.

1. Нахождение спектральной плотности одиночного видео- и радиоимпульса

Исходный видеоимпульс показан на рис. 1.1. Его длительность τ = 6 мкс. Спектральную плотность этого видеоимпульса можно найти разными способами. Для данного случая удобнее всего воспользоваться теоремами о спектрах.

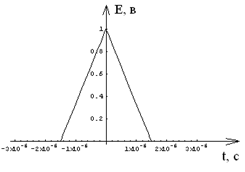
Рисунок 1.1 – Видеоимпульс.

Известно, что спектральная плотность прямоугольного видеоимпульса расположенного симметрично вертикальной оси представляет собой [1]:

(1.1)

Для получения спектральной плотности заданного сигнала воспользуемся теоремами о сдвиге во времени и о дифференцировании во времени [1]:

(1.2)

Как видно конечное выражение спектральной плотности (1.2) чисто действительное, это означает, что аргумент спектральной плотности видеосигнала на всех частотах равен нулю. Модуль спектральной плотности видеосигнала представлен на рис. 1.2.

Для нахождения спектральной плотности одиночного радиоимпульса воспользуемся теоремой о спектре модулированного сигнала [1]:

(1.3)

После подстановки выражения спектральной плотности видеоимпульса получим:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--