Курсовая работа: Анализ частотных свойств линейных избирательных цепей
7. Расчет зависимости коэффициента демодуляции от модулируемой частоты
Как известно график коэффициента демодуляции повторяет нормированную правую ветвь амплитудно-частотной характеристики избирательной цепи. Коэффициент демодуляции рассчитывается по формуле:
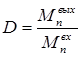 (7.1)
(7.1)
Где ![]() - коэффициент модуляции n-той гармоники на входе цепи.
- коэффициент модуляции n-той гармоники на входе цепи.
![]() - коэффициент модуляции n-той гармоники на выходе цепи.
- коэффициент модуляции n-той гармоники на выходе цепи.
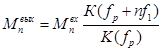 (7.2)
(7.2)
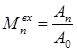 (7.3)
(7.3)
Для расчета коэффициента демодуляции по формуле (7.1) необходимо найти коэффициенты модуляции гармоник на входе и выходе избирательной цепи. Как видно из формулы (7.3) для расчетов необходимо знать коэффициент А0 . Его можно найти из формулы из формулы (7.3) для первой гармоники сигнала. По заданию имеем коэффициент модуляции первой гармоники спектра сигнала на входе М1 = 80 %. Тогда А0 = 0.09. Тогда можно найти коэффициенты модуляции гармоник сигнала на входе по формуле (7.3). Значения коэффициентов модуляции первых девяти гармоник сигнала на входе избирательной цепи приведены в таблице 7.1. Для расчета коэффициента модуляции на выходе цепи необходимы коэффициенты Аn на выходе цепи. В данной курсовой работе рассчитывались коэффициенты Сn на выходе цепи. Воспользуемся формулой (7.4) для перехода к коэффициентам Аn :
![]()
![]() (7.4)
(7.4)
Коэффициенты модуляции на выходе цепи а также коэффициенты демодуляции для первых девяти гармоник сигнала приведены в таблице (7.1)
Таблица 7.1 – Значения коэффициентов модуляции на входе и выходе избирательной цепи и коэффициентов демодуляции для первых десяти гармоник сигнала.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0.8 | 0.7895 | 0.7722 | 0.7485 | 0.7189 | 0.6840 | 0.6445 | 0.6011 | 0.5548 | 0.5065 | |
| 0.7833 | 0.7294 | 0.6566 | 0.5783 | 0.5024 | 0.4329 | 0.3707 | 0.3159 | 0.2678 | 0.2257 | |
| D | 0.9791 | 0.9239 | 0.8504 | 0.7726 | 0.6989 | 0.6329 | 0.5752 | 0.5255 | 0.4826 | 0.4456 |
Для сравнения на рисунке 7.1 приведена нормированная амплитудно-частотная характеристика контура и построенные по точкам коэффициенты демодуляции. Как видно точки рассчитанные по формула (7.1) – (7.4) полностью совпадают с нормированной АЧХ избирательной цепи.
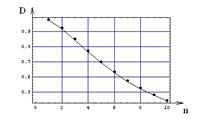
Рисунок 7.1 – Зависимость коэффициента демодуляции от частоты.
8. Отклик цепи при воздействии одиночного радиоимпульса
Расчет отклика избирательной цепи на воздействии на ее вход одиночного радиоимпульса произведем методом огибающей. Метод огибающей коротко можно представить как перемножение низкочастотного эквивалента избирательной цепи и удвоенной части спектральной плотности радиоимпульса на положительных частотах [1].
В пункте 1 данной курсовой работы была найдена спектральная плотность радиоимпульса. Для расчетов необходимо выделить удвоенную правую часть спектральной плотности. График удвоенной части спектральной плотности на положительных частотах радиоимпульса приведен на рис. 8.1.
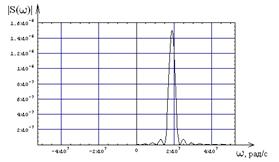
Рисунок 8.1 – Удвоенная положительная часть спектральной плотности радиоимпульса.
Низкочастотный эквивалент избирательной цепи можно получить сдвинув максимум АЧХ цепи в ноль т.е. взяв в качестве аргумента функции не частоту ω, а частоту (ω - ωрез ):
 (8.1)
(8.1)
График низкочастотного эквивалента цепи приведен на рис. 8.2.
Перемножая спектральную плотность радиоимпульса и низкочастотный эквивалент цепи, получаем:
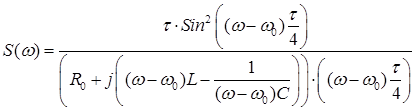 (8.2)
(8.2)
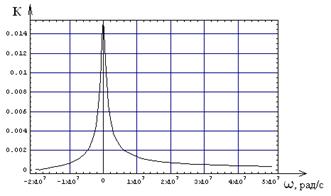
Рисунок 8.2 – НЧ эквивалент избирательной цепи.
Результат перемножения и есть спектральная плотность радиоимпульса на выходе избирательной цепи, при воздействии одиночного радиоимпульса с треугольной огибающей (формула 8.2). График спектральной плотности выходного сигнала приведен на рисунке 8.3.
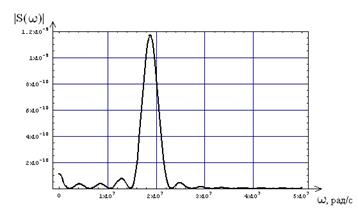
Рисунок 8.3 – Спектральная плотность сигнала на выходе.