Курсовая работа: Анализ частотных свойств линейных избирательных цепей
где:
ω0 = 2 π f0 = 1.88873·107 рад/с
Как видно спектральная плотность одиночного радиоимпульса также является чисто действительной величиной, поэтому её аргумент на всех частотах равен нулю. Зависимость модуля спектральной плотности от частоты приведена на рис. 1.3
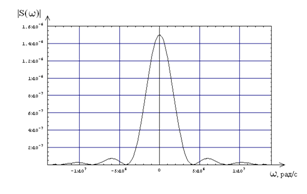
Рисунок 1.2 – Зависимость модуля спектральной плотности одиночного видеосигнала от частоты.
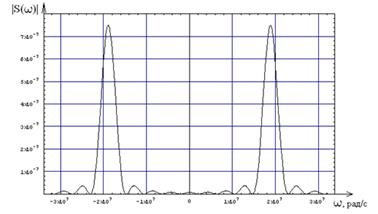
Рисунок 1.3 – Зависимость модуля спектральной плотности одиночного радиосигнала от частоты.
2. Расчет АЧС и ФЧС периодических видеоимпульсов
Для расчета амплитудно-частотного и фазочастотного спектров периодической последовательности видеоимпульсов (рис. 2.1) воспользуемся формулами для нахождения коэффициентов а0 /2 и аn (2.1, 2.2).

Рисунок 2.1 – Периодическая последовательность видеоимпульсов.
Так как в задании не указан момент начала отсчета времени, примем для простоты – пик видеоимпульса находится в точке t= 0. Тогда сигнал становиться четным, это означает что коэффициенты bn = 0 [2].
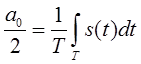 (2.1)
(2.1)
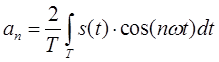 (2.2)
(2.2)
Аналитическое выражение сигнала имеет вид:
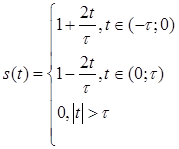 (2.3)
(2.3)
Подставляя аналитическое выражение сигнала (2.3) в формулы (2.1), (2.2) получаем:
![]() ,
, 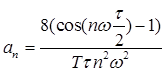 (2.4)
(2.4)
Таким образом, аналитическое выражение периодического видеосигнала имеет вид:
 (2.5)
(2.5)
На рис. 2.2 приведена зависимость первых 30 коэффициентов Аn от частоты.

Рисунок 2.2 – Зависимость коэффициентов Аn от частоты (n– множитель частоты первой гармоники)
Для анализа прохождения сигнала через избирательную цепь перейдем к коэффициентам Сn . Как известно из [1] переход от коэффициентов Аn к Сn происходит по следующей формуле:
![]()
![]() (2.6)
(2.6)
Фазовый спектр на положительных частотах сохраняется.
Для проверки вычислим коэффициенты Сn по формуле [2]:
 (2.7)
(2.7)
Значения коэффициентов Сn для гармоник от -5 до 5 приведены в таблице (2.1), а графики модулей и аргументов приведены на рис. 2.3 и 2.4 соответственно. Как видно из вычислений и графиков фазы спектральных составляющих на всех частотах равны нулю.