Курсовая работа: Анализ эмпирического распределения

Вариационные ряды распределения состоят из двух элементов: вариантов и частот. Вариантом называется числовое значение количественного признака в ряду распределения. Они могут быть положительными и отрицательными, абсолютными и относительными.

Частоты – это численности отдельных вариантов или каждой группы вариационного ряда, т.е. числа, показывающие, как часто встречаются те или иные варианты в вариационном ряду. Сумма всех частот равна общему количеству элементов совокупности и называется объемом совокупности.

Частости – это частоты, выраженные в виде относительных величин (в долях единицы или процентах). Сумма частостей равна единице или 100%.

Первым шагом к упорядочиванию первичного ряда данных является его ранжирование, т.е. расположение всех его данных в возрастающем или убывающем порядке.

Способы построения дискретного и интервального вариационных рядов различны, поэтому, вначале нужно определить к какому типу относится исследуемый ряд данных. Поскольку исходными данными для анализа являются данные о числе легковых автомобилей на 1000 человек населения, то вариационный ряд будет интервальным (так как значения признака могут быть дробными).

Следовательно, в первую очередь необходимо определить количество групп и интервалы группировки.

Интервал – количественное значение, отделяющее одну единицу (группу) от другой, т.е. интервал очерчивает количественные границы групп[2] .

Ориентировочно определить оптимальное количество групп с равными интервалами можно по формуле Стерджесса:

, (1.1)

где N – численность единиц совокупности.

Формула Стерджесса пригодна при условии, что распределение единиц совокупности по данному признаку приближается к нормальному и при этом применяются равные интервалы в группах.

Численность единиц совокупности равна 80, следовательно по формуле Стерджесса количество групп вариационного ряда будет равно:

Однако поскольку формула Стерджесса дает приемлемые результаты только при анализе больших совокупностей, рассмотрим несколько различных вариантов распределения с различным количеством интервалов.

Ниже приведены таблицы вариационного ряда, построенные с использованием разного количества интервалов (рис. 1.1.).

Выбирая окончательный вариант табличного представления вариационного ряда из представленных вариантов, остановимся на первом – n=8. При n=13 наблюдает много малонаполненных групп и нулевой интервал, при n=10 также имеются малонаполненные группы.

В таблицах первая непоименованная графа (From To) содержит интервалы значений признака «Количество легковых автомобилей на 1000 чел. населения».

Второй столбец «Count» – абсолютные частоты (f_i ), т.е. число единиц совокупности, обладающих указанным значением признака.

Cumulative Count – накопленные абсолютные частоты, получаемые последовательным суммированием частот по группам. Сумма накопленных частот по каждой строке означает, какое количество единиц совокупности (регионов) имеет значение признака, не превышающее значения верхней границы данного интервала. Общая сумма накопленных частот соответствует объему изучаемой совокупности (80).

Percent – частости (относительные частоты, w_i ; выражаются в процентах), рассчитываются:

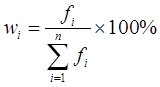, (1.2)

где:f_i – число единиц i-той группы; – общее число единиц в совокупности; w_i – доля каждой группы в общем объеме совокупности.

а)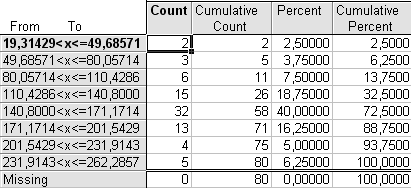

б)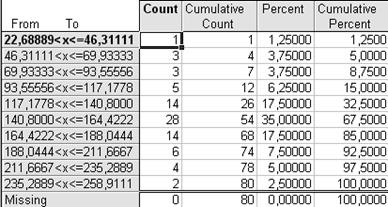

в)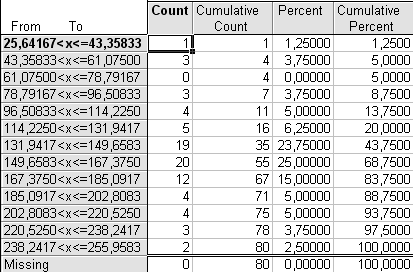

Рис. 1.1. Распределение регионов России по значению показателей «Количество легковых автомобилей на 1000 человек населения» в 2005 г. с числом интервалов а) n=8, б) n=10, в) n=13

Cumulative percent – накопленные частости – это результат последовательного суммирования относительных частот по группам, итоговая сумма, очевидно, равна 100%.

Табличное представление вариационного ряда позволяет получить подробную информацию о составе и структуре изучаемой совокупности, т.е. определить какое количество единиц изучаемой совокупности обладает тем или иным значением признака и какова доля этой группы единиц в общем объеме совокупности, а также выявить закономерность изменения частот.

Из таблицы видно, что наибольшую частоту (32 или 40,0% от всего объема совокупности) имеет интервал 140,8-171,2 автомобилей на 1000 чел. населения.