Курсовая работа: Анализ эмпирического распределения

Для более наглядного представления вариационного ряда используют статистические графики.

Статистический график представляет собой чертеж, на котором при помощи условных геометрических фигур (линий, точек или других символических знаков) изображаются статистические данные. В результате этого достигается наглядная характеристика изучаемой статистической совокупности.

Правильно построенный график делает статистическую информацию более выразительной, запоминающейся и удобно воспринимаемой[3] .

Традиционно для изображения вариационных рядов распределения в отечественной практике используются графики: гистограмма, полигон, кумулята.

На рис. 1.2 представлен полигон распределения регионов России по количеству легковых автомобилей на 1000 чел. населения за 2005 г. в абсолютных частотах при количестве интервалов n=8. Он показывает, что наибольшую частоту имеет интервал 140,8-171,17, т.е. это модальный интервал.

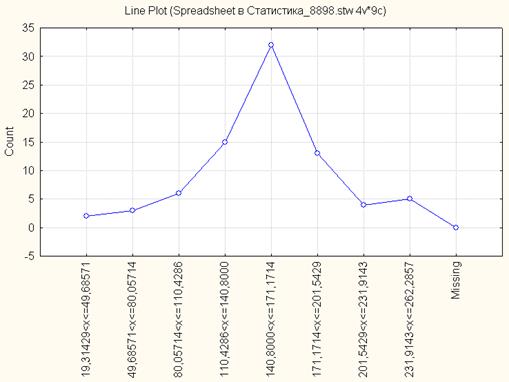
Рис. 1.2. Полигон распределения регионов России по количеству легковых автомобилей на 1000 чел. населения за 2005 г. в абсолютных частотах (n=8)

На рис. 1.3 приведена кумулята распределения в абсолютных частотах, а на рис. 1.4. – в относительных частотах.

Из рисунка 1.2 видно, что середина распределения приходится на интервал 140,8-171,17, следовательно, этот интервал является медианным.

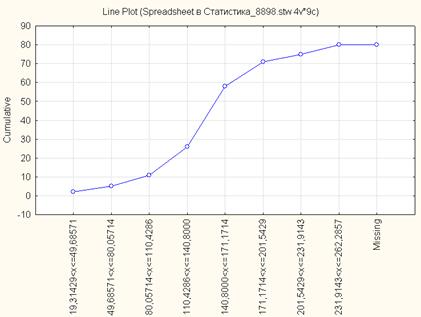
Рис. 1.3. Кумулята распределения регионов России по количеству легковых автомобилей на 1000 чел. населения за 2005 г., n=8 (абсолютные частоты)

Одной из часто используемых видов графиков является гистограмма (или столбиковая диаграмма), т.е. график распределения, на котором частоты каждого интервала представлены в виде столбиков (рис. 1.5).

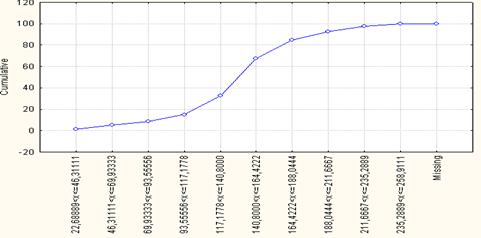
Рис. 1.4. Кумулята распределения регионов России по количеству легковых автомобилей на 1000 чел. населения за 2005 г., n=8 (относительные частоты)

Рис. 1.5. Гистограмма распределения количества легковых автомобилей на 1000 чел. населения по регионам России за 2005 г. (n=8)

2. ХАРАКТЕРИСТИКА ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ

РАСПРЕДЕЛЕНИЯ

Статистический анализ вариационных рядов распределения предполагает расчет характеристик центра распределения, его структуры, оценку степени вариации и дифференциации изучаемого признака, изучение формы распределения.

В качестве показателей центральной тенденции распределения используются: среднее арифметическое значение, мода и медиана.

Средней арифметической величиной называется такое значение признака в расчете на единицу совокупности, при вычислении которого общий объем признака в совокупности сохраняется неизменным.

Иными словами, средняя арифметическая величина — среднее слагаемое. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности[4] .

Средняя арифметическая определяется по формулам:

1) Средней арифметической простой (для несгруппированных данных):

,(2.1)

где: – значение признака у i-й единицы совокупности; n – объем совокупности (ValidN).

2) Средней арифметической взвешенной (для интервального вариационного ряда):

, (2.2)

где:f_i – абсолютные частоты; x_i – середина интервала.