Курсовая работа: Анализ эмпирического распределения

где:N – объем совокупности; h – величина интервала.

Из рис. 6.1. видно, что критерий для нормального распределения составил 5,42808 при количестве степеней свободы 2 и расчетном уровне значимости 0,06627.

Для принятия решения о справедливости гипотезы о законе распределения необходимо сравнить рассчитанный критерий с критическим значением.

Табличное значение для степеней свободы r=2 и уровня значимости α=0,05 составляет 5,991. Поскольку рассчитанное значение меньше табличного, то гипотеза о нормальном распределении переменной Var1 не противоречит статистическим данным.

На рис. 6.2 показана гистограмма эмпирического распределения и расчетная кривая нормального распределения для исследуемой переменной.

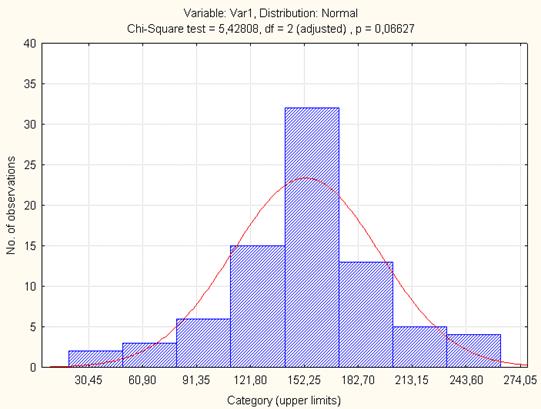
Рис. 6.2. Гистограмма и расчетная кривая нормального распределения для переменной Var1

В табл. 6.1 приведен расчет теоретических частот для сглаживания эмпирических данных нормальным распределением.

Расчетное значение критерия Пирсона составило . Табличное значение критерия – .

Таблица 6.1 Расчет критерия вручную

№
1.	19,31	49,69	34,50	-2,666	0,0114	1	1,000
2.	49,69	80,06	64,87	-1,982	0,0559	3	0,000
3.	80,06	110,43	95,24	-1,299	0,1716	9	1,000
4.	110,43	140,80	125,61	-0,615	0,3302	18	0,500
5.	140,80	171,17	155,99	0,068	0,3980	23	3,522
6.	171,17	201,54	186,36	0,752	0,3007	16	0,563
7.	201,54	231,91	216,73	1,436	0,1424	8	2,000
8.	231,91	262,29	247,10	2,119	0,0422	2	4,500
Итого:							13,084

Очевидно, что расчетное значение критерия превышает критическое, следовательно гипотеза о нормальном распределении подтверждена (табл. 6.2).

Таблица 6.2 Проверка гипотезы о нормальном законе распределения вручную

Тип распределения	Число степеней свободы r	Расчетное значение критерия	Табличное значение критерия
Нормальное	7	13,084	14,07

Рассмотрим также гипотезы о логнормальном и прямоугольном распределении (рис. 6.2 и рис. 6.3).

Из рис. 6.2 видно, что критерий для логнормального распределения равен 16,48145 при количестве степеней свободы r=3 и уровне значимости 0,0009.

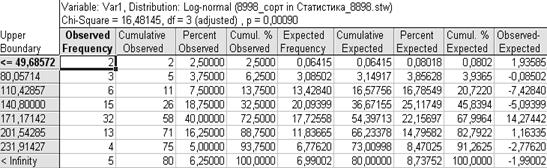
Рис. 6.2. Проверка гипотезы о логарифмически нормальном распределении переменной Var1

Сопоставим рассчитанные показатели с табличным значением критерия Пирсона:

Очевидно, что расчетное значение критерия Пирсона превышает критическое, а расчетная вероятность ниже табличного уровня значимости. Следовательно, гипотеза о логнормальном распределении вариационного ряда не может быть принята.

На рис. 6.3 приведена гистограмма и расчетная кривая логнормального распределения переменной Var1.

На рис. 6.4 приведена таблица расчета теоретических частот и критерия Пирсона для прямоугольного распределения.

Таким образом, расчетный критерий Пирсона для прямоугольного распределения составил 54,48687 при количестве степеней свободы 5 и вероятности 0,00:

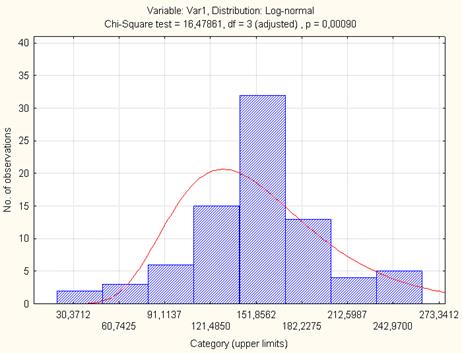
Рис. 6.3. Гистограмма и расчетная кривая логнормального распределения для переменной Var1

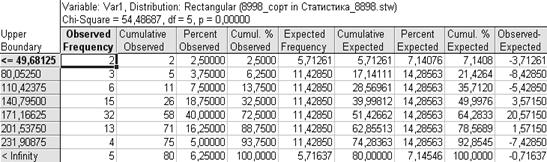
Рис. 6.4. Проверка гипотезы о прямоугольном распределении переменной Var1