Курсовая работа: Анализ эмпирического распределения

Таблица 5.2 Расчет ассиметрии и эксцесса для распределения регионов России по количеству легковых автомобилей на 1000 чел. населения за 2005 г.

Интервал	Абсолютная частота (fi )	Середина интервала (xi )
19,31429-49,68571	1	34,5	-3323682,13	393685400,9
49,68571-80,05714	3	58,12	-2049797,54	180540318,8
80,05714-110,4286	3	81,74	-1152941,93	66531323,0
110,4286-140,8	5	105,365	-306347,11	8373775,1
140,8-171,1714	14	128,99	896,48	2722,7
171,1714-201,5429	28	152,61	484749,46	16194790,2
201,5429-231,9143	14	176,23	1037801,06	66190981,2
231,9143-262,2857	6	199,855	4173022,64	392896041,5
Итого:	80	–	-1136299,06	1124415353,4

Коэффициент ассиметрии по сгруппированным данным:

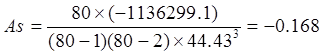
Коэффициент ассиметрии на основе исходного ряда данных был рассчитан с помощью ППП Statistica и составил -0,341.

Коэффициент эксцесса на основе сгруппированных данных:

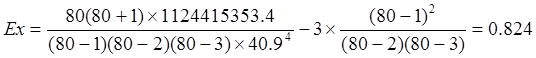
Коэффициент эксцесса, рассчитанный для несгруппированных данных, составил 1,075.

Сопоставим показатели, рассчитанные вручную по сгруппированным данным, и показатели, полученные с помощью программы Statistica на основе исходного ряда данных (табл. 5.3).

Таблица 5.3 Сравнение статистических показателей, рассчитанных различными способами

№	Название показателя	Значение в ППП Statistica	Значение после ручного расчета
1.	Средняя арифметическая	153,055	152,95
2.	Медиана	153,45	154,09
3.	Мода	161,70	155,14
4.	Дисперсия	1730,257	1973,99
5.	Нижний квартиль	135,85	128,65
6.	Верхний квартиль	172,75	175,84

6. СГЛАЖИВАНИЕ ЭМПИРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ.

ПРОВЕРКА ГИПОТЕЗЫ О ЗАКОНЕ РАСПРЕДЕЛЕНИЯ

Одна из важнейших задач анализа вариационных рядов заключается в выявлении закономерности распределения и определении ее характера. Основной путь в выявлении закономерности распределения – построение вариационных рядов для достаточно больших совокупностей. Важное значение для выявления закономерности распределения имеет правильное построение самого вариационного ряда: выбор числа групп и размера интервала варьирующего признака.

Говоря о характере, типе закономерности распределения, имеем в виду отражение в нем общих условий вариации. При этом речь всегда идет о распределениях качественно однородных явлений. Общие условия, определяющие тип закономерности распределения, познаются анализом сущности явления, тех его свойств, которые определяют вариацию изучаемого признака. Следовательно, должна быть выдвинута какая-то научная гипотеза, обосновывающая тип теоретической кривой распределения.

Под теоретической кривой распределения понимается графическое изображение ряда в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариантов (значений признака).

Теоретическое распределение может быть выражено аналитически – формулой, которая связывает частоты вариационного ряда и соответствующие значения признака. Такие алгебраические формулы носят название законов распределения[6] .

Процедура выравнивания, сглаживания анализируемого распределения заключается в замене эмпирических частот теоретическими, определяемыми по формуле теоретического распределения, но с учетом фактических значений переменной. На основе сопоставления эмпирических и теоретических частот рассчитываются критерии согласия, которые используются для проверки гипотезы о соответствии исследуемого распределения тому или иному типу теоретического распределении.

Для проверки статистической гипотезы о законе распределения будем использовать критерий – критерий Пирсона (Chi-square test). Расчет критерия производится по следующей формуле:

(6.1)

где: – эмпирические абсолютные частоты (Observed Frequency); – абсолютные частоты теоретического распределения (Expected Frequency); k – число интервалов.

С помощью ППП Statistica проведем сглаживание рассматриваемого распределения и проверим статистическую гипотезу о законе распределения.

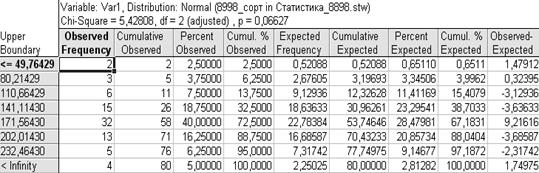
Рис. 6.1. Проверка гипотезы о нормальном распределении переменной Var1

Для сглаживания эмпирического распределения переменной Var1 нормальным распределением необходимо использовать формулы, приведенные ниже.

Функция нормального распределения:

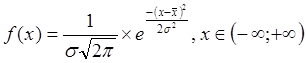(6.2)

Плотность нормального распределения определяется по формуле:

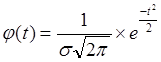(6.3)

где:х – значение изучаемого признака; – средняя арифметическая величина; – среднее квадратическое отклонение изучаемого признака; – математические константы; 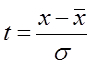– нормированное отклонение.

Теоретические частоты нормального распределения рассчитываются по следующей формуле: