Курсовая работа: Анализ режимов автоматического управления
Для этого необходимо найти корни характеристического уравнения передаточной функции звена Т3 , Т4 .
![]() (1.6)
(1.6)
![]()
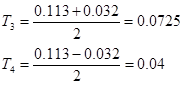
Тогда передаточная функция апериодического звена второго порядка запишется следующим образом:
![]() (1.7)
(1.7)
![]()
 Уравнение асимптотической ЛАЧХ для апериодического звена второго порядка имеет вид
Уравнение асимптотической ЛАЧХ для апериодического звена второго порядка имеет вид
L ( ω) ≈
Первая асимптота начинается в точке 20 lgk и продолжается до точки сопрягающей частоты ω1 =1/ T3 - начало второй асимптоты, которая откладывается с наклоном - 20дБ/дек. Третья асимптота начинается в точке сопрягающей частотыω2 =1/ T3 и имеет наклон уже - 40дБ/дек. В результате получим характеристику, изображенную на рис.2.

Рисунок 2. Амплитудная частотная характеристика апериодического звена второго порядка
1.3 Построение логарифмической фазовой частотной характеристики
Рассмотрим построение ЛФЧХ для апериодического звена второго порядка. Так как это звено можно представить в виде двух апериодических звеньев первого порядка, соединенных последовательно, то общая ЛФЧХ φ (ω) будет представлять собой сумму фазовых частотных характеристик апериодических звеньев первого порядка (рис.3).
φ (ω ) = - arctg ω T3 - arctg ω T4 ( 1.9)
![]()
ЛФЧХ в этом случае при ω→0 асимптотически стремится к оси частот, а при ω→∞ - к прямой φ= =-2π.
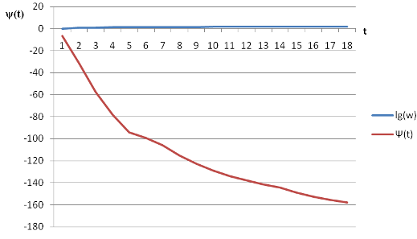
Рисунок 3. Логарифмическая фазовая частотная характеристика
1.4 Временные характеристики САУ
Важной характеристикой автоматических систем (звеньев) является переходные и импульсные переходные функции и их графики - временные характеристики.
Переходной функцией системы (звена) называют функцию, описывающую изменение выходной величины системы (звена), когда на ее вход подается единичное ступенчатое воздействие при нулевых начальных условиях. Другими словами, переходная функция h ( t) есть функция, описывающая реакцию системы (звена) на единичное ступенчатое воздействие при нулевых начальных условиях.
При построении графика (рис.4) переходной функции апериодического звена второго порядка используется зависимость
 (1.10)
(1.10)
где Т3 и Т4 корни характерестического уравнения передаточной функции (1.6).
Подставив заданные параметры колебательного звена k=19,35 Т1 =0,0725, Т2 =0,04, получим следующее выражение:
![]()
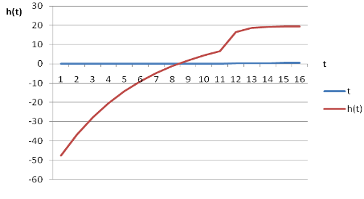
Рисунок 4. Переходная функция апериодического звена второго порядка
Импульсной переходной, или весовой, функцией системы (звена) называют функцию, описывающую реакцию системы (звена) на единичное импульсное воздействие при нулевых начальных условиях.
Весовая и переходная функции связаны между собой следующим образом:
ω ( t) = h ( t) ' (1.11)