Курсовая работа: Анализ режимов автоматического управления
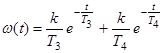 (1.12)
(1.12)
![]()

Рисунок 5. Весовая характеристика апериодического звена второго порядка
1.5 Исследование устойчивости САУ
Устойчивость - это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.
Критерий устойчивости Рауса-Гурвица.
Это алгебраический критерий, по которому условия устойчивости сводятся к выполнению ряда неравенств, связывающих коэффициенты уравнения системы. В разной форме этот критерий был предложен английским математиком Е. Раусом и затем швейцарским математиком А. Гурвицем в конце прошлого века. Приведем без доказательства этот критерий в форме Гурвица.
Возьмем характеристический полином, определяющий левую часть уравнения системы,
D ( l) = a0 l n + a1 l n - 1 + … + an -1 l+ an (1.13)
где полагаем a0 > 0 , что всегда можно обеспечить умножением при необходимости полинома на - 1. Составим из коэффициентов этого полинома определитель
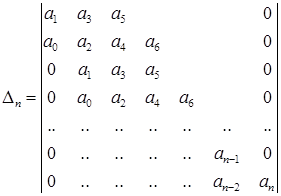 (1.14)
(1.14)
Этот определитель называется определителем Гурвица. Он имеет п строк и п столбцов. Первая строка содержит все нечетные коэффициенты до последнего, после чего строка заполняется до положенного числа п элементов нулями. Вторая строка включает все четные коэффициенты и тоже заканчивается нулями. Третья строка получается из первой, а четвертая - из второй сдвигом вправо на один элемент. На освободившееся при этом слева место ставится нуль. Аналогично сдвигом вправо на элемент получаются все последующие нечетные и четные строки из предыдущих одноименных строк.
Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров.
Развернем критерий Гурвица для нескольких конкретных значений п.
Для n=2

Условия устойчивости:
a0 > 0; a1 > 0; a2 > 0
( к последнему неравенству сводится неравенство D2 > 0 , если учесть предыдущее неравенство а1 > 0 ).
Подставляя данные значения в уравнение имеем:
![]() ;
;
![]()
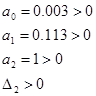
Можно сделать вывод, что система устойчивая.
2. Синтез системы "объект-регулятор"
2.1 Расчет оптимальных параметров регуляторов
Согласно заданию, передаточная функция объекта управления имеет вид:
![]() (2.1)
(2.1)
К = 100;
Т1 = 0,03;
Т2 = 8.9;