Курсовая работа: Анализ системы автоматического регулирования разрежения в топке

;

Полученный результат показывает, что система устойчива.

5.2 Анализ устойчивости по критерию Найквиста

Передаточная функция разомкнутой системы:

;

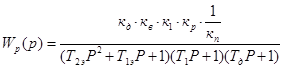Частотная передаточная функция разомкнутой системы:

;

Для построения АФЧХ разомкнутой системы рассчитаем значения А (w) и φ (w); тогда используя

;

;

Передаточная функция в виде:

;

Без преобразований получаем:

;

;

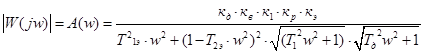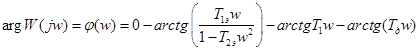Таблица 2. значения А (w) и φ (w).

Подставим численные значения.

;

;

Строим на комплексной плоскости АФЧХ разомкнутой системы: (рис.5)

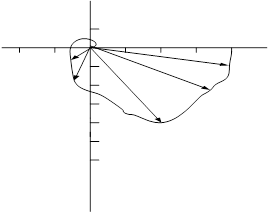
Рис.5. АФЧХ разомкнутой цепи

Таблица 2. - Результаты расчёта.

w	0	0.01	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1	1.5	1.8	1.9	2.5	4
A (w)	2	1.99	1.69	1.44	1.23	1.03	0.88	0.75	0.64	0.55	0.48	0.25	0.15	0.13	0.076	0.018
φ (w)	0	-5.2	4.63	6.45	80.7	94.3	106.3	117	127	137	145	181	216	221	-245	-260

Вывод: По критерию Найквиста система устойчива.

5.3 Определение запасов устойчивости

По АФЧХ разомкнутой системы определяем запас устойчивости по фазе Δφ, и запас устойчивости по амплитуде - ΔА. , что удовлетворяет величинам запаса устойчивости по фазе и амплитуде.

Для рассматриваемой системы разрежение в топке Δφ и ΔА удовлетворяет рекомендуемым величинам запасов по фазе и амплитуде устойчивости.

6. Анализ зависимости статической ошибки системы от изменения управляющего воздействия на систему

Передаточная функция для ошибки по управляющему воздействию.

;

в статике Р обращается в ноль, поэтому:

;