Курсовая работа: Анализ цепи во временной области различными методами
![]()
Таким образом:

Совпадение полюсов функции передачи ![]() и
и ![]() с собственными значениями матрицы
с собственными значениями матрицы ![]() -
- ![]() и
и ![]() даёт дополнительную информацию о правильности нахождения передаточной функции.
даёт дополнительную информацию о правильности нахождения передаточной функции.
Аналогично из числителя функции передачи находятся нули функции:
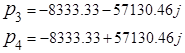
Наиболее наглядным способом охарактеризовать передаточную функцию является графическое расположение ее полюсов и нулей на комплексной плоскости, называемой диаграммой полюсов-нулей (рис.3.1).
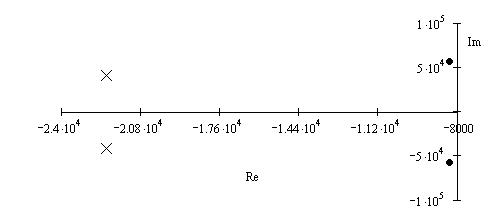
Рисунок 3.1. Диаграмма полюсов-нулей.
Так как полюсы передаточной функции лежат в левой полуплоскости, в линейной пассивной цепи имеются резистивные элементы, в результате чего будет происходить затухание свободной составляющей напряжения. Передаточные функции, полюса которых не лежат в правой полуплоскости комплексной плоскости, называются устойчивыми.
Нули передаточной функции при учете потерь могут располагаться в любой части комплексной плоскости.
4.2 Определение переходной и импульсной характеристик
Переходная характеристика цепи представляет собой реакцию цепи на воздействие единичной ступенчатой функции (функции Хэвисайда 1 (t) ) и может быть найдена как обратное преобразование Лапласа от![]() , либо с помощью формулы разложения:
, либо с помощью формулы разложения:
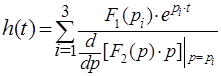 , (8) где
, (8) где ![]() и
и ![]() числитель и знаменатель передаточной функции
числитель и знаменатель передаточной функции ![]() соответственно, а
соответственно, а ![]() - корни выражения
- корни выражения ![]() :
:
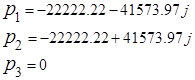
Таким образом, подставляя корни ![]() и, применяя преобразование Эйлера, получим:
и, применяя преобразование Эйлера, получим:
![]()
Импульсная характеристика цепи ![]() представляет собой реакцию цепи на воздействие единичной импульсной функции
представляет собой реакцию цепи на воздействие единичной импульсной функции ![]() и может быть найдена как обратное преобразование Лапласа от передаточной функции, либо с помощью формулы разложения:
и может быть найдена как обратное преобразование Лапласа от передаточной функции, либо с помощью формулы разложения:
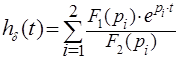 , (9) где
, (9) где ![]() и
и ![]() числитель и знаменатель передаточной функции
числитель и знаменатель передаточной функции ![]() соответственно, а
соответственно, а ![]() - полюсы
- полюсы ![]() :
:

Таким образом:
![]()
Первое слагаемое определяется действием на входе цепи d - импульса тока и существует только для t=0 . В дальнейшем переходной процесс протекает за счет энергии, накопленной в электрическом поле конденсатора и магнитном поле индуктивности в результате действия d - импульса тока. Из приведенного выражения видно, что, как и в первом случае, переходной процесс носит затухающий колебательный характер с частотой, равной собственной частоте рассматриваемой цепи: w св = 41574 рад/сек.Подобного вида решения (с d -функцией) возникают всякий раз, когда степени полиномов числителя и знаменателя передаточной функции оказываются равными. Коэффициент при ![]() соответствует части входного импульса поступающей в нагрузку.
соответствует части входного импульса поступающей в нагрузку.
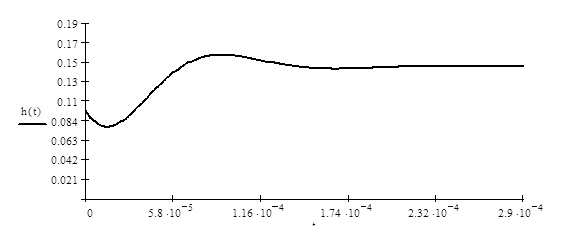 |
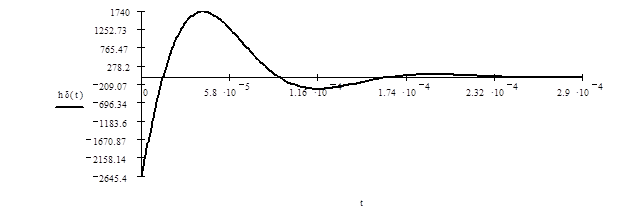
Рисунок 3.2. Импульсная и передаточная характеристики
4.3 Определение напряжения на нагрузке
Входной импульс в данном задании представляет собой знакопеременное прямоугольное напряжение. Его можно представить как сумму следующих функций:
![]()
Применяя теорему Запаздывания, найдём операторное изображение для одиночного импульса напряжения: