Курсовая работа: Анализ цепи во временной области различными методами

Так как , выразим :

(11)

Подставив в (11) выражения (10) и (7), получим:

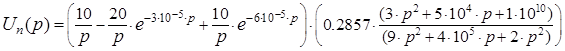
Для того чтобы найти оригинал этой функции, воспользуемся таблицами для преобразований Лапласа:

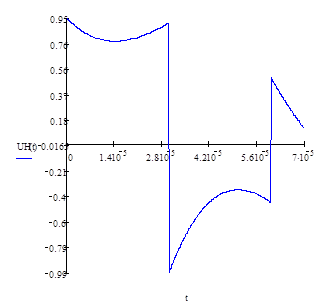
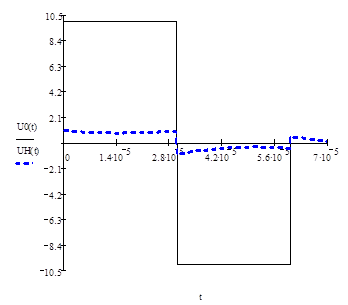
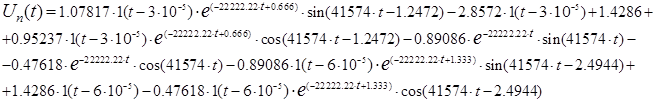
Рисунок 3.3 Графики входного и Рисунок 3.4 График выходного

выходного сигналов сигнала

5. Анализ цепи частотным методом при апериодическом воздействии

5.1 Определение амплитудно-фазовой (АФХ), амплитудно-частотной (АЧХ)и фазо-частотной (ФЧХ) характеристик функции передачи

Амплитудно-частотная характеристика – это зависимость от частоты модуля входной, выходной или передаточной функции цепи, выраженных в комплексной форме (ГОСТ 19880-74 ). Амплитудно-частотная характеристика (АЧХ) является одной из самых важных характеристик любой цепи и позволяет исследовать искажения вносимые цепью в спектр входного сигнала. Наличие частотно - зависимых элементов (L и C ) в исследуемой цепи приводит к неравномерному изменению составляющих спектра входного сигнала. Наиболее простой способ получения АЧХ цепи - это замена в выражении для операторной переменной p на мнимую частоту jw и нахождение модуля полученной комплексной функции частоты:

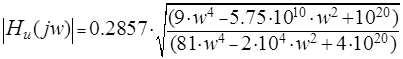
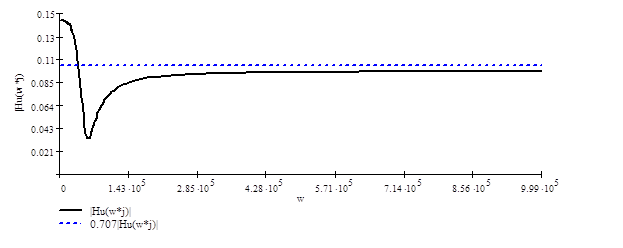Рисунок 4.1 АЧХ функции передачи по напряжению

Характеристика имеет вид, качественно сходный с подобной характеристикой параллельного колебательного контура. По построенной характеристике может быть определена полоса пропускания. Полоса пропускания – полоса частот, в пределах которой затухание остаётся ниже определённого значения (СТ МЭК 50(151)-78 ). Т. е. коэффициент передачи для этой полосы не более чем в отличается от его максимального значения. Для рассматриваемой цепи максимальное значение передаточной функции достигается на нулевой частоте (для постоянного напряжения) и составляет . Границе полосы пропускания соответствует значение передаточной функции . Это значение достигается на частоте . Таким образом, полоса пропускания равна: .

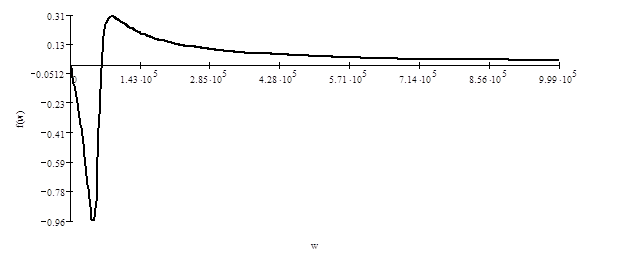????-????????? ?????????????? ? ??????????? ?? ??????? ????????? ???????, ???????? ??? ???????????? ??????? ????, ?????????? ? ??????????? ????? (ГОСТ 19880-74 ). ????? ???????, ??? ?????? ???? ??? ????? ????? ???: . ??????????? ?? ??????? ????????? ??? ????? ???, ?????????????? ?? ???. 4.2.

Рисунок 4.2 ФЧХ функции передачи по напряжении

Амплитуднофазочастотная характеристика цепи (годограф) связывает воедино изменение коэффициента передачи (в нашем случае, по напряжению - ) и фазового сдвига между выходным и входным напряжением во всем диапазоне частот. Годограф включает сведения, которые содержатся как в АЧХ, так и в ФЧХ.

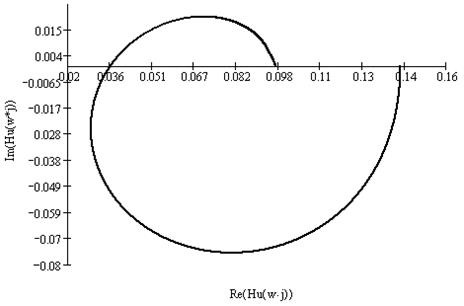
Рисунок 4.3 Годограф анализируемой цепи

Годограф является параметрической кривой, параметром которой является частота w . Длина вектора, проведенного из начала координат к какой-либо точке годографа, соответствует абсолютному значению передаточной функции на этой частоте , а угол между ним и положительным направлением вещественной оси - аргументу передаточной функции . Нулевой частоте (постоянному напряжению) соответствует точка с координатой 0.1428 на вещественной оси, очень большой (в пределе бесконечной) частоте соответствует точка с координатой 0.09524 на вещественной оси. На этих граничных частотах влияние реактивных элементов на фазовый сдвиг отсутствует.

5.2 Определение амплитудного и фазового спектра входного сигнала

Для нахождения спектральной характеристики входного сигнала можно воспользоваться непосредственно прямым преобразованием Фурье. Второй путь решения этой задачи основан на аналогии между преобразованиями Лапласа и Фурье и состоит в замене в операторном изображении входного сигнала (10) операторной переменной p на мнимую частоту jw . В итоге после простых преобразований получим:

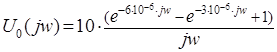
Амплитудный спектр входного сигнала может быть найден как модуль спектральной характеристики сигнала:

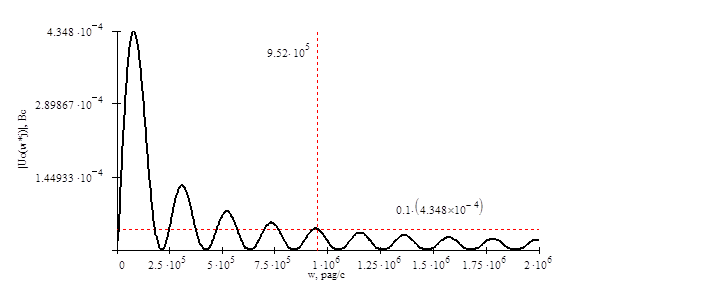
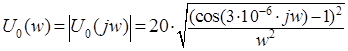
Рисунок 4.4 АЧХ входного сигнала

Максимальное значение спектральной характеристики достигается при и составляет . Определенная по уровню ширина спектра сигнала составляет . Между шириной спектра сигнала и его длительностью существует следующее соотношение: . Для данного вида сигнала получаем: . Эта константа называется базой сигнала. Уменьшение длительности импульса в 100 раз приводит к такому же (в 100 раз) увеличению ширины его спектра. Наличие широкого спектра у коротких импульсов дает возможность использования таких импульсов для исследования частотных свойств различных цепей. В математическом смысле спектр несинусоидального сигнала неограничен.

Фазовый спектр входного сигнала определяется как аргумент от входной спектральной характеристики: .

Рисунок 4.5 Фазовый спектр входного сигнала