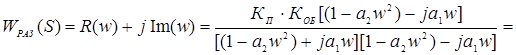Курсовая работа: Автоматизация вельц печи для переработки цинковых кеков
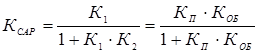
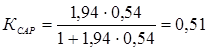
Принимая величину изменения задания yЗ = 1, находим установившееся значение
yуст = 1 . 0,51 = 0,51
Тогда статическая ошибка равна
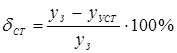
![]()
Для уменьшения статической ошибки и сохранения других показателей качества регулирования необходимо применять другие законы регулирования (например И- или ПИ- закон).
4 Исследование устойчивости системы регулирования
Под устойчивостью понимают свойство системы самостоятельно возвращаться к равновесному состоянию после снятия возмущения, нарушевшего ее равновесие.
Устойчивость линейной системы определяется характером его свободного движения, которое описывается однородным дифференциальным уравнением
![]()
При вещественных корнях решение имеет вид
y(t)= c1 . eP1t + c2 . eP2t + …+ cn . ePnt ,
где cn – постоянная интегрирования
pn – корни характеристического уравнения
an . pn + an -1 . pn -1 + …+a0 = 0
Для устойчивой работы системы необходимо, чтобы Pi <0
Решение характеристического уравнения сложно, поэтому разработаны другие критерии устойчивости.
Частотным критерием Найквиста определяют устойчивость замкнутой системы по поведению соответствующей ей разомкнутой системы.
Если в разомкнутом состоянии система устойчива и ее амплитудно-фазовая характеристика (АФХ) при изменении частоты W от нуля до бесконечности не охватывает на комплексной плоскости точку с координатами (-1;0), то система в замкнутом состоянии будет устойчива. АФХ охватывает точку, если точка лежит внутри контура, образованного характеристиками и отрезками действительной оси, соединяющей точки ноль и бесконечность.
Выполним исследование системы на устойчивость. Определим АФХ разомкнутой системы с П-регулятором. Для получения передаточной функции приведем рисунок 4.
 |
Рисунок 4 – Функциональная схема разомкнутой системы регулирования
Передаточная функция разомкнутой системы будет иметь вид
WРАЗ (S) = WP (S) . WОБ (S)
Выполняя замену WР = КП , WОБ (S) = jw получим
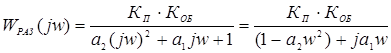
Избавляясь от мнимости в знаменателе, получим АФХ в алгебраической форме