Курсовая работа: Численные методы решения типовых математических задач

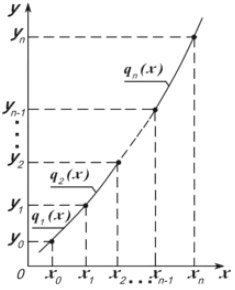
Например, для некоторых функций (рис.) необходимо задать все кубические функции q₁ (x), q₂ (x), …q_n (x).

В наиболее общем случае эти многочлены имеют вид:

где k_ij - коэффициенты, определяемые описанными ранее условиями, количество которых равно 4n. Для определения коэффициентов kij необходимо построить и решить систему порядка 4n.

Первые 2n условий требуют, чтобы сплайны соприкасались в заданных точках:

Следующие (2n-2) условий требуют, чтобы в местах соприкосновения сплайнов были равны первые и вторые производные:

Система алгебраических уравнений имеет решение, если число уравнений соответствует числу неизвестных. Для этого необходимо ввести еще два уравнения. Обычно используются следующие условия:

При построении алгоритма метода первые и вторые производные удобно аппроксимировать разделенными разностями соответствующих порядков.

Полученный таким образом сплайн называется естественным кубическим сплайном. Найдя коэффициенты сплайна, используют эту кусочно-гладкую полиноминальную функцию для представления данных при интерполяции.

2.4 Численный метод решения задачи

Значения f(x₀ ), f(x₁ ), … , f(x_n ) , т.е. значения табличной функции в узлах, называются разделенными разностями нулевого порядка (k=0).

Отношение называется разделенной разностью первого порядка (k=1) на участке [x₀ , x₁ ] и равно разности разделенных разностей нулевого порядка на концах участка [x₀ , x₁ ], разделенной на длину этого участка.

Для произвольного участка [x_i , x_i+1 ] разделенная разность первого порядка (k=1) равна

Отношение называется разделенной разностью второго порядка (k=2) на участке [x₀ , x₂ ] и равно разности разделенных разностей первого порядка, разделенной на длину участка [x₀ , x₂ ].

Для произвольного участка [x_i , x_i+2 ] разделенная разность второго порядка (k=2) равна

Таким образом, разделенная разность k-го порядка на участке [x_i , x_i+k ] может быть определена через разделенные разности (k-1)-го порядка по рекуррентной формуле:

(2.3)

Где n – степень многочлена.

Максимальное значение k равно n. Тогда i =0 и разделенная разность n-го порядка на участке [x₀ ,x_n ] равна

,

т.е. равна разности разделенных разностей (n-1)-го порядка, разделенной на длину участка [x₀ ,x_n ].

Разделенные разности

являются вполне определенными числами, поэтому выражение (2.2) действительно является алгебраическим многочленом n-й степени. При этом в многочлене (2.2) все разделенные алгебраическим многочленом n-й степени. При этом в многочлене (2.2) все разделенные разности определены для участков [x₀ , x_0+k ], .