Курсовая работа: Численные методы решения типовых математических задач

Метод простых итераций (1.19) сходится к единственному решению СЛАУ при любом начальном приближении x⁽⁰⁾ , если какая-либо норма матрицы α эквивалентной системы меньше единицы

Если используется метод Якоби (выражения (1.18) для эквивалентной СЛАУ), то

достаточным условием сходимости является диагональное преобладание матрицы A, т.е.

(для каждой строки матрицы A модули элементов, стоящих на главной диагонали, больше суммы модулей недиагональных элементов). Очевидно, что в этом случае ||α||_c меньше единицы и, следовательно, итерационный процесс (1.19) сходится.

Приведем также необходимое и достаточное условие сходимости метода простых итераций. Для сходимости итерационного процесса (1.19) необходимо и достаточно, чтобы спектр матрицы α эквивалентной системы лежал внутри круга с радиусом, равным единице.

При выполнении достаточного условия сходимости оценка погрешности решения на k- ой итерации дается выражением:

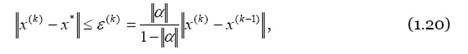
где x^· - точное решение СЛАУ.

Процесс итераций останавливается при выполнении условия , где εε≤)(kε - задаваемая вычислителем точность.

Принимая во внимание, что из (1.20) следует неравенство , можно получить априорную оценку необходимого для достижения заданной точности числа итераций. При использовании в качестве начального приближения вектора β такая оценка определится неравенством:

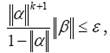
откуда получаем априорную оценку числа итераций k при ||α||<1

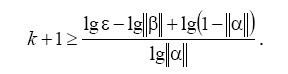
Следует подчеркнуть, что это неравенство дает завышенное число итераций k, поэтому редко используется на практике.

1.6 Текст программы

program Yakobi;

uses crt;

const

maxn=100;

type

matrix=array[1..maxn,1..maxn] of real;

vector=array[1..maxn] of real;

vector1=array[1..maxn] of real;

var

i,j,n,k1: integer;

e,norma:real;

a: matrix;

b: vector;

x2,x3: vector1;

imya,dannble_i_rezultat,ekran:string;