Курсовая работа: Численные методы решения типовых математических задач

В терминах матричных операций такая операция эквивалентна умножению A(k)=MkA(k-1), где элементы матрицы определяются следующим образом

В результате прямого хода метода Гаусса получим , A(n-1)=U

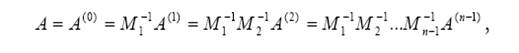
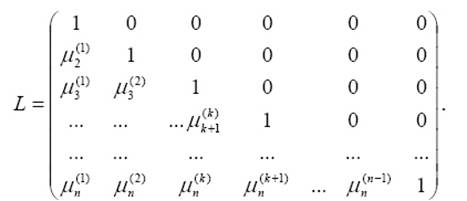
где A(n-1)=U - верхняя треугольная матрица, а - нижняя треугольная матрица, имеющая вид .

Таким образом, искомое разложение A=LU получено.

Метод прогонки

Метод прогонки является одним из эффективных методов решения СЛАУ с трех - диагональными матрицами, возникающих при конечно-разностной аппроксимации задач для обыкновенных дифференциальных уравнений (ОДУ) и уравнений в частных производных второго порядка и является частным случаем метода Гаусса. Рассмотрим следующую СЛАУ:

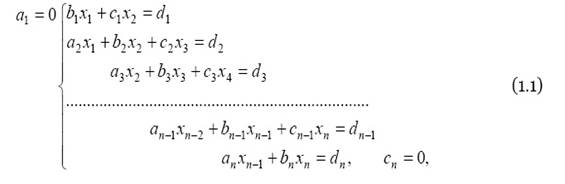
решение которой будем искать в виде

где Qi,Pi,i=1,n - прогоночные коэффициенты, подлежащие определению. Для их определения выразим из первого уравнения СЛАУ (1.1) x1 через x2, получим:

откуда

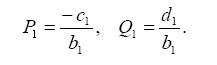
Из второго уравнения СЛАУ (1.1) с помощью (1.3) выразим x2 через x3, получим:

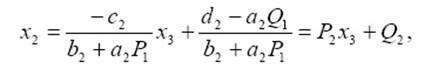
откуда

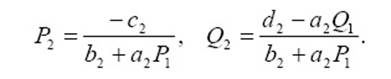
Продолжая этот процесс, получим из i-го уравнения СЛАУ (1.1):

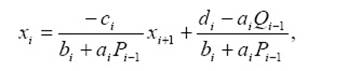
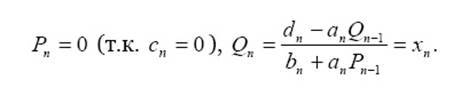
следовательно

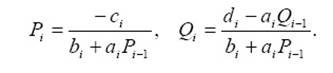
Из последнего уравнения СЛАУ имеем

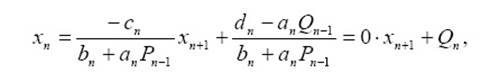
то есть

Метод простых итераций

При большом числе уравнений прямые методы решения СЛАУ (за исключением метода прогонки) становятся труднореализуемыми на ЭВМ прежде всего из-за сложности хранения и обработки матриц большой размерности. В то же время характерной особенностью ряда часто встречающихся в прикладных задачах СЛАУ является разреженность матриц. Число ненулевых элементов таких матриц мало по сравнению с их размерностью. Для решения СЛАУ с разреженными матрицами предпочтительнее использовать итерационные методы.

Методы последовательных приближений, в которых при вычислении последующего приближения решения используются предыдущие, уже известные приближенные решения, называются итерационными.

Метод Зейделя решения СЛАУ