Курсовая работа: Динамічні процеси та теорія хаосу

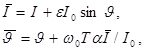(1.22)

де позначено

(1.23)

Рівняння (1.22) називають також стандартним відображенням зважаючи на його максимальну простоту.

Приведемо також вид гамильтониана, відповідного спрощеному відображенню (1.22):

(1.24)

Лінійний член ? ₀ I у гамильтонианеH зникає при ? ₀ = 0. Квадратичний член по дії I при цьому залишається, оскільки через визначення (1.23) величина ?? ₀ відмінна від нуля при ? ₀ = 0.

Структура фазового простору . Запишемо систему (1.22) в спрощеній формі, опустивши постійне зрушення фази ?₀ T і перейшовши до безрозмірної дії:

Отримуємо (1.25)

Нерухомі точки системи (1.25) знаходяться з рівнянь тобто

Звідси знаходимо особливі крапки

Точки r1 є нестійкими крапками. Поведінка траєкторій поблизу них показує, що ці точки гіперболічного типа.

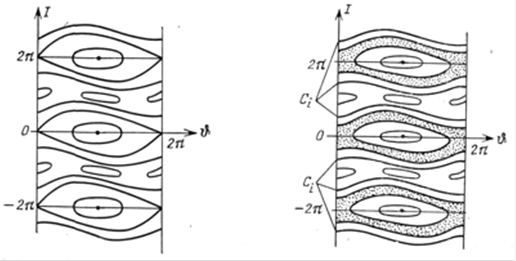
Рис. 1.6. Фазовий портрет стандартного відображення при малих значеннях K

Рис. 1.7. Фазовий портрет стандартного відображення при K : 1;Ci – інваріантні криві

Точки r 2 є еліптичними, якщо К0 < 4. Фазовий портрет системи для малих K0 приведений на мал. 1.6. Із зростанням К0 в системі відбуваються біфуркації народження кратних періодів, а при K0 поблизу одиниці з'являється в околиці сепаратрисыширокий стохастичний шар (мал. 1.7). Різні стохастичні шари відокремлені один від одного інваріантними кривими, що існують унаслідок теореми Колмогорова—арнольда—мозера.

Стохастичне море . Подальше збільшення параметра K0 приводить до руйнування КАМ-КРІВИХ і злиттю стохастичних шарів. Утворюється стохастичне море, в якому, проте, існують острівці стійкості (мал. 1.8). Острівці залишаються завжди при будь-яких скільки завгодно великих значеннях K0 . Їх розмір в цьому випадку має порядок 1/K0, а відображення (1.25) із зростанням К0 стає все ближчим до У-системе.

Наявність острівців стійкості є фундаментальною властивістю реальних фізичних систем. Все сказане вище без зусиль переноситься на універсальне відображення (1.20), і відзнака виражається кінець кінцем лише у формі і числі острівців.

Сама структура острівців також є незвичайно складною заплутаною картиною. Існують системи острівців різних порядків розмірів, що все більш і більш зменшуються (мал. 1.9). Утворення стохастичного шару відбувається в околиці сепаратрисы при K0 < 0,97, а в області значень K0 > 0,97 відбувається злиття стохастичних шарів з утворенням спільного стохастичного моря. Таким чином, область переходу до хаосу є дуже вузькою.

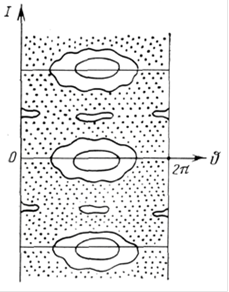
Рис. 1.8. Утворення стохастичного моря

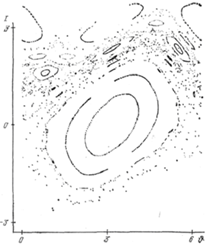
Рис. 1.9. Острівці різних порядків в стохастичному морі. Окремі, безладно розташовані крапки належать одній траєкторії

У міру подальшого зростання параметра K0 > 1 стохастичне море заповнює все велику частку фазового простору. В той же час острівці стійкості зменшуються в своїх розмірах. Одночасно зменшується і відносна міра острівців.

1.4 Стохастичні аттрактор и

Відзначимо деякі істотні сторони появи стохастичності в негамильтоновских диссипативних системах. Існування дисипації приводить до зменшення фазового об'єму системи.

Фінітность руху. Наступне нижче зауваження перш за все відноситься до поняття локальної нестійкості. Очевидно, що поява цієї нестійкості формулюється настільки універсальним способом, що він не пов'язаний з конкретним детальним видом динамічної системи.