Курсовая работа: Дослідження топологічного визначення верхніх напівґрат

Нехай ґрати, тоді її найбільший елемент характеризуються одним із властивостей:

1.

2..

Аналогічно характеризується найменший елемент :

1.

2..

3. Дистрибутивні ґрати

Визначення: Ґрати називаються дистрибутивної , якщо для виконується:

1.

2.

У будь-яких ґратах тотожності (1) і (2) рівносильні. Доказ цього факту втримується в книзі [1], стор. 24.

Теорема: Ґрати з 0 і 1 є дистрибутивною тоді й тільки тоді, коли вона не містить у

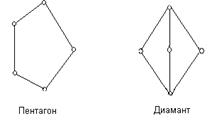
Доказ цього факту можна знайти в книзі [2].

Далі під словом “ґрати” розуміється довільні дистрибутивні ґрати з 0 і 1 (причому ).

Визначення: Непуста множина називається ідеалом у ґратах , якщо виконуються умови:

1.

2.

Визначення: Ідеал у ґратах називається простим , якщо

або .

Ідеал, породжений множиною Н (тобтонайменший ідеал, що містить H ), буде позначатися (Н]. Якщо Н = {a} , то замість ({a}] будемо писати (a] і називати (a] головним ідеалом.

Позначимо через I(L) множина всіх ідеалів ґрати L. I(L) будемо називати ґратами ідеалів.

Визначення: Ґрати й називаються ізоморфними (позначення: ), якщо існує взаємно однозначне відображення , називане ізоморфізмом, множини на множину , таке, що

,

.

4. Топологічні простори

Визначення: Топологічний простір – це непуста множина з деякою системою виділених його підмножин, що задовольняє аксіомам:

Порожня множина й сам простір належить системі : .

Перетинання будь-якого кінцевого числа множин з належить , тобто .