Курсовая работа: Дослідження топологічного визначення верхніх напівґрат
![]() .
.
Нехай ![]() , тобто
, тобто ![]() (мал.3), для деяких
(мал.3), для деяких ![]()
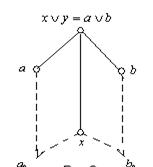
Зрозуміло, що ![]() . По дистрибутивності, існують
. По дистрибутивності, існують ![]() такі, що
такі, що ![]() . Т.к. A – ідеал, те
. Т.к. A – ідеал, те![]() , тому що
, тому що ![]() . Аналогічно,
. Аналогічно, ![]() . Т.е.
. Т.е. ![]() . Точно також,
. Точно також, ![]() . Якщо
. Якщо ![]() , то легко показати, що
, то легко показати, що ![]() .
.
Довели, що ![]() - ідеал. Очевидно, він є верхньою гранню ідеалів A і B. Якщо C містить A і B , то C буде містити елементи
- ідеал. Очевидно, він є верхньою гранню ідеалів A і B. Якщо C містить A і B , то C буде містити елементи ![]() для будь-яких
для будь-яких ![]() , тобто
, тобто ![]() Тому
Тому ![]() , оскільки
, оскільки ![]() є верхньою гранню ідеалів A і B і втримується в будь-який верхній грані.
є верхньою гранню ідеалів A і B і втримується в будь-який верхній грані.
Тепер покажемо, що виконується рівність:
![]() .
.
![]() . Нехай
. Нехай ![]() , де
, де ![]() ,
,![]() .
. ![]() , те
, те![]() , звідки
, звідки ![]() й отже
й отже ![]() . Аналогічно,
. Аналогічно, ![]() , виходить,
, виходить, ![]()
![]() . Нехай
. Нехай ![]() ,де
,де ![]()
![]()
![]()
![]()
![]() .
.
Звідси треба дистрибутивність ґрати ![]() .
.
![]()
![]() – дистрибутивні ґрати,
– дистрибутивні ґрати, ![]() . Тепер розглянемо ідеали, утворені цими елементами:
. Тепер розглянемо ідеали, утворені цими елементами:
![]()
(![]() ,буде нижньою границею для
,буде нижньою границею для ![]() ). Тому
). Тому ![]() , що й доводить дистрибутивність напівґрат
, що й доводить дистрибутивність напівґрат ![]() . :
. :
2. Стоуновий простір
Визначення : Підмножина ![]() верхніх напівґрат
верхніх напівґрат ![]() називається коідеалом , якщо
називається коідеалом , якщо ![]() з нерівності
з нерівності ![]() треба
треба ![]() й
й ![]() існує нижня границя
існує нижня границя ![]() множини
множини ![]() , така, що
, така, що ![]() .
.
Визначення: Ідеал ![]() напівґрати
напівґрати ![]() називаються простим , якщо
називаються простим , якщо ![]() й множина
й множина ![]() є коідеалом.
є коідеалом.
Надалі нам буде потрібно лема Цорна, що є еквівалентним твердженням аксіомі вибору.
Лема Цорна. Нехай A – множина й X – непуста підмножина множини P(A). Припустимо, що X має наступну властивість: якщо C – ланцюг в <![]() >, те
>, те ![]() . Тоді X має максимальний елемент.
. Тоді X має максимальний елемент.
Лема 2 : Нехай ![]() – довільний ідеал і
– довільний ідеал і ![]() – непустий коідеал дистрибутивних верхніх напівґрат
– непустий коідеал дистрибутивних верхніх напівґрат ![]() . Якщо
. Якщо ![]() , то в напівґратах
, то в напівґратах ![]() існує простий ідеал
існує простий ідеал ![]() такий, що
такий, що ![]() й
й ![]() .
.
Доказ.
Нехай X – множина всіх ідеалів в L, що містять I і не пересічних з D . Покажемо, що X задовольняє лемі Цорна.
Нехай C – довільний ланцюг в X і ![]() Якщо
Якщо ![]() , те
, те ![]() для деяких
для деяких ![]() Нехай для визначеності
Нехай для визначеності ![]() . Тоді
. Тоді ![]() й
й ![]() , тому що
, тому що ![]() - ідеал. Тому
- ідеал. Тому ![]() . Обернено, нехай
. Обернено, нехай ![]() , тоді
, тоді ![]() , для якогось
, для якогось ![]() Одержуємо
Одержуємо ![]() , звідки
, звідки ![]() .
.
Довели, що M – ідеал, мабуть, що містить I і не пересічний з D , тобто ![]() . По лемі Цорна X має максимальний елемент, тобто максимальним ідеалом P серед утримуючих I і не пересічних з D.
. По лемі Цорна X має максимальний елемент, тобто максимальним ідеалом P серед утримуючих I і не пересічних з D.
Покажемо, що P – простій. Для цього досить довести, що L\P є коідеалом. Нехай ![]() L\P і
L\P і ![]() . Оскільки
. Оскільки ![]() , те
, те![]() , інакше в противному випадку
, інакше в противному випадку ![]() по визначенню ідеалу. Отже,
по визначенню ідеалу. Отже, ![]() . Якщо
. Якщо ![]() , то
, то ![]() й
й ![]() пересічних з D у силу максимальності P. Одержуємо
пересічних з D у силу максимальності P. Одержуємо ![]() й
й ![]() для деяких елементів
для деяких елементів ![]() . Існує елемент
. Існує елемент ![]() такий, що
такий, що ![]() й
й ![]() , по визначенню коідеала, отже
, по визначенню коідеала, отже ![]() й
й ![]() для деяких
для деяких ![]() Помітимо, що
Помітимо, що ![]() й
й ![]() не лежать в P, тому що в противному випадку
не лежать в P, тому що в противному випадку ![]() .
.
Далі, ![]() , тому
, тому ![]() для деяких
для деяких ![]() і
і ![]() . Як і колись
. Як і колись ![]() . Крім того
. Крім того ![]() , тому
, тому ![]() - нижня грань елементів a і b, що не лежить в P . :
- нижня грань елементів a і b, що не лежить в P . :
Надалі, через ![]() будемо позначати дистрибутивні верхні напівґрати з нулем, через
будемо позначати дистрибутивні верхні напівґрати з нулем, через ![]() множину всіх простих ідеалів напівґрати
множину всіх простих ідеалів напівґрати ![]() .
.
Множини виду ![]() представляють елементи напівґрат
представляють елементи напівґрат ![]() у ч.в. множині
у ч.в. множині ![]() (тобто
(тобто ![]() ). Зробимо всі такі множини відкритими в деякій топології.
). Зробимо всі такі множини відкритими в деякій топології.
Позначимо через ![]() топологічний простір, певний на множині
топологічний простір, певний на множині ![]() . Простір SpecL будемо називати стоуновим простором напівґрат L.
. Простір SpecL будемо називати стоуновим простором напівґрат L.
Лема 3 : Для будь-якого ідеалу I напівґрати L покладемо: