Курсовая работа: Дослідження зміни температури термопари за допомогою чисельних методів на ЕОМ
Дослідження зміни температури термопари за допомогою чисельних методів на ЕОМ.
В приведеній тарировочній таблиці для термопари дані показання вольтметра при зміні температури з постійним кроком:
| Т0 | 0 | 20 | 40 | 60 | 80 | 100 |
| QмВ | -0,670 | -0,254 | 0,171 | 0,609 | 1,057 | 1,517 |
Використовуючи інтерполяцію по Лагранжу і Ньютону, знайти показання вольтметра при Т0 =270 ; 320 ; 550 ; 750 ; 670 С. Оцінити похибку методів інтерполяції [1,3] . Зробити висновки.
Анотація
В даній курсовій роботі розроблено комплекс програм для дослідження зміни температури термопари за допомогою чисельних методів на ЕОМ. Розроблення даного програмного продукту є не тільки практичним втіленням теоретичного аналізу ринку сучасних прикладних програм, але актуальною і потрібною вимогою часу. В програмі додержані основні сучасні вимоги до інтерфейсу користувача та логічної структури програми, що дозволяє з впевненістю сказати про те, що дана програма знайде своє практичне комерційне застосування.
Зміст
Вступ
1.Огляд і варіантний аналіз чисельних методів моделювання зміни температури термопари
1.1 Основні поняття і визначення
1.2 Класифікація методів рішення поставленої задачі
1.3.Опис методів моделювання зміни температури термопари на ЕОМ
1.3.1. Інтерполяційний многочлен Лагранжа
1.3.2 .Перший інтерполяційний многочлен Ньютона
1.3.3. Другий інтерполяційний многочлен Ньютона
1.3.4. Інтерполювання функцій за схемою Ейткіна
1.3.5. Сплайн-інтерполяція
1.4. Уточнена постановка задачі
2. Розробка алгоритмів моделювання зміни температури термопари за допомогою чисельних методів на ЕОМ
2.1. Планування вхідних та вихідних даних
2.2 Аналіз задач, які вирішуються при дослідженні зміни температури термопари на ЕОМ
2.3 Описовий алгоритм головної програми
2.4 Схема алгоритму головної програми
2.5 Опис основних функцій моделювання
2.6 Структура комплексу програм для дослідження зміни температури термопари
3. Лістинг програми.
3.1 Лістинг головної програми INTERP.CPP
3.2 Лістинг модуля MENYS.H
4. Розробка тестів та аналіз результату тестування
4.1 Опис тестів
4.2 Аналіз результатів тестування
5. Оцінка похибок результатів експериментальних досліджень
6. Оцінка ефективності комплексу програм для дослідження
7. Розробка пакету документів для супроводження комплексу програм
7.1 Розробка інструкції програмісту
7.2 Інструкція користувачеві
Висновки
Використана література
Додаток А. Технічне завдання.
Додаток Б. Лістинги модулів
Додаток В. Структура дискети.
Вступ
Сучасний розвиток науки та техніки тісно пов’язаний із застосуванням ЕОМ, які дають змогу будувати математичні моделі складних систем, пристроїв та процесів, тим самим різко скоротити час та коштовність інженерних розробок.
Складні обчислювальні задачі, які виникають при моделюванні розбивають на елементарні: обчислення інтегралів, розв’язання системи лінійних та нелінійних алгебраїчних та диференційних рівнянь, визначення екстремуму функції.Для таких задач вже розроблені ефективні методи розв’язання.
В наш час науково-технічний прогрес невідривно пов’язаний з бурхливим розвитком систем управління і автоматики. Автоматика – це галузь науки і техніки, яка охоплює теорію та принципи побудови систем управління процесами, що діють без безпосередньої участі людини. У відповідності до загальних принципів управління різними процесами, автоматичне управління здійснюється на основі інформації з використанням комплексу технічних засобів.
Автоматизація технологічних процесів на основі застосування автоматизованих станків, машин та механізмів, робототехнічних комплексів, сучасних засобів автоматики та обчислювальної техніки складає один з головних напрямків науково технічного прогресу в усіх галузях народного господарства. Вирішення задач автоматизації в наш час неможливе без застосування досягнень мікроелектроніки, яка забезпечує випуск елементної бази для пристроїв автоматики та систем управління в цілому.
1 Огляд і варіантний аналіз чисельних методів моделювання термопари
1.1 Основні поняття та визначення
Нехай на відрізку [а; b] визначено певний клас функцій {Р(х)}, наприклад клас алгебраїчних многочленів, а в точках х0 , х1 ,..., хn цього проміжку задано значення деякої функції y=f(x): y0 =f(x0 ), y1 =f(x1 ),….yn =f(xn ).
Інтерполяція – це наближена заміна функції f на відрізку [а; b] однією з функцій Р(х) цього класу так, щоб функція P(х) в точках x0 ,x1 , ..., xn набувала тих самих значень, що й функція f, тобто щоб Р(xi )= уi (і = 0, 1, ..., n). На Рис.1.1.1 зображена інтерполяція функції.
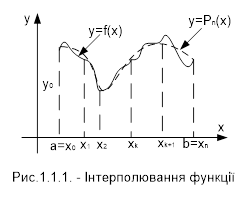
Вузли інтерполювання – це точки х0 , хi , ..., хn , в яких задана функція.
Функція Р(х) називається інтерполюючою функцією .
Інтерполяційна формула – це формула у=P(х), за допомогою якої обчислюють значення функції f у проміжку [а;b].
Якщо функція Р(х) належить класу алгебраїчних многочленів, то інтерполювання називається параболічним . Параболічне інтерполювання найзручніше, оскільки многочлени, які прості за формою і не мають особливих точок, можуть набувати довільних значень, їх легко обчислювати, диференціювати й інтегрувати.
Інтерполяційний многочлен – це многочлен виду Рn (х), який задовольняє умови ![]()
![]() , наближену рівність f(x)=Pn (x) називають інтерполяційною формулою , а різницю Rn (f,x)=f(x) – Pn (x) — залишковим членом інтерполяційної формули. Хоч інтерполяційний многочлен і єдиний, проте можливі різні форми його запису. Інтерполяційний поліном має слідуючий вид:
, наближену рівність f(x)=Pn (x) називають інтерполяційною формулою , а різницю Rn (f,x)=f(x) – Pn (x) — залишковим членом інтерполяційної формули. Хоч інтерполяційний многочлен і єдиний, проте можливі різні форми його запису. Інтерполяційний поліном має слідуючий вид:
![]() ( 1.1)
( 1.1)
При обробці результатів вимірювань часто виникає необхідність побудови емпіричної формули, більш простішої, чим інтерполяційний поліном, яка б добре відображала фізичні властивості досліджуваного процесу.
В цьому випадку необхідно рішити задачу відшукання оптимальних в деякому випадку оцінок параметрів системи.
Апроксимація – це наближений опис однією функцією (апроксимувальною) заданого вигляду іншої функції (апроксимовної), яка задається у будь-якому вигляді (при апроксимації даних вона задається у вигляді масивів даних).
Нехай у таблиці задана ![]() точка
точка ![]() і треба знайти апроксимувальну криву
і треба знайти апроксимувальну криву ![]() в діапазоні
в діапазоні ![]() (рисунок 1.1.2.). В цьому випадку похибка в кожній табличній точці буде
(рисунок 1.1.2.). В цьому випадку похибка в кожній табличній точці буде ![]() Тоді сума квадратів похибок визначається виразом:
Тоді сума квадратів похибок визначається виразом:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--