Курсовая работа: Дослідження зміни температури термопари за допомогою чисельних методів на ЕОМ

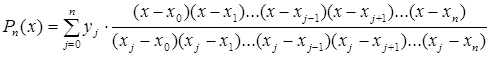(1.8)

Формулу (1.8) називають інтерполяційний многочлен Лагранжа.

Треба відзначити дві головні властивості поліномів Лагранжа:

1) 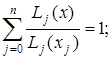(1.9)

2) якщо лінійно залежить від , то слушний принцип суперпозиції: інтерполяційний поліном суми декількох функцій дорівнює сумі інтерполяційних поліномів доданків.

Похибка при інтерполяції за Лагранжем може бути оцінена таким чином:

(1.10)

де .

1.3.2 Перший інтерполяційний многочлен Ньютона.

Інтерполяційний поліном випадку має вигляд:

...

...+, (1.11)

Коефіцієнти знаходять з рівнянь:

,, (1.12)

(1.13)

Формула (1.13) носить назву першої інтерполяційної формули Ньютона. Цей вираз незручний для інтерполяції поблизу останніх значень .

Похибка інтерполяції для першої формули Ньютона можна оцінити відповідно як: (1.14)

де (1.15)

1.3.3 Другий інтерполяційний многочлен Ньютона

В випадку, коли, першу інтерполяційну формулу Ньютона застосувати незручно, використовують другу інтерполяційну формулу Ньютона, яка отримана при використанні лівих різниць від останнього значення (інтерполяція “назад”). Тоді інтерполяційний поліном має вигляд:

(1.16)

Коефіцієнти визначаються таким чином:

, (1.17)

(1.18)

– ліва різниця першого порядку в точці ,

(1.19)

– ліва різниця другого порядку.