Курсовая работа: Единое пересечение кривых в пространстве

Обе эти распадающиеся кривые проходят через четыре точки M₁ , M₂ , M₃ , M₄ не имеют других общих точек; между тем у них должна была бы быть еще и пятая общая точка, а именно точка M₅ . Противоречие! Итак, утверждение доказано: из четырех точек M₁ , M₂ , M₃ , M₄ три, пусть M₁ , M₂ , M₃ , лежат на одной прямой d .

Докажем, что на той же прямой d лежит и четвертая точка (M₄ или M₅ ). Пусть ни M₄ , ни M₅ не лежат па прямой d .

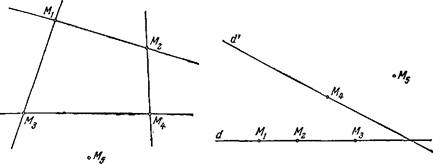
Проведем через точку M₄ произвольную прямую d' , не проходящую через точку M₅ . Имеем снова кривую второго порядка, а именно пару прямых d и d' , проходящую через точки M₁ , M₂ , M₃ , M₄ , но не проходящую через M₁ , — опять получили противоречие.

Итак, мы доказали: если уравнения (2) зависимы, то из точек M₁ , M₂ , M₃ , M₄ , M₅ четыре лежат на одной прямой. Теорема 1 доказана.

Теорема2 (теорема единственности) . Если два уравнения второй степени

F ( x , y ) = a ₁₁ x ² + 2 a ₁₂ 2 xy + a ₂₂ y ² + 2 a ₁ x + 2 a ₂ y + a ₀ = 0 (3)

и

F′(x, y) =a′₁₁ x² + 2a′₁₂ 2xy + a′₂₂ y² + 2a′₁ x + 2a′₂ y + a′₀ = 0 (4)

удовлетворяются одним и тем же множеством точек С комплексной плоскости, то одно из этих уравнений получается из другого почленным умножением на некоторой числовой множитель.

Добавление к теореме 2. Если известно лишь, что множество действительных точек плоскости, удовлетворяющих уравнениям, (3) и (4), одно и то же и состоит более чем из одной точки, то Утверждение теоремы2 остается в силе (каждое из уравнений (3), (4) получается из другого умножением на числовой множитель).

Докажем сначала частный случай этой теоремы, а именно случай, когда множество всех точек, удовлетворяющих уравнению (3), есть некоторая прямая d (т. е. когда линия, определяемая этим уравнением, есть пара совпадающих, непременно действительных, прямых). Перейдя к системе координат, осью ординат которой является прямая d , можем предположить, что ее уравнение есть х = 0 . Достаточно доказать, что в этом случае F(x, у) = a ₁₁ x ² .

Уравнение (3), по предположению, удовлетворяется точками M =(0, у) при любом у , и только этими точками. Поэтому, подставив в (3) значение х=0 , получим тождество относительно у :

a ₂₂ y ² + 2а₂ у + a ₀ = 0.

Это значит, что a ₂₂ = a ₂ = a ₀ = 0 и уравнение (3) имеет вид

F(x, у) = х( a ₁₁ х + 2 a ₁₂ y + 2 a ₁ ) = 0 . (5)

Оно удовлетворяется, кроме точек оси ординат, еще и всеми точками прямой d' :

a ₁₁ х + 2 a ₁₂ y + 2 a ₁ = 0.

Но уравнение (5) должно удовлетворяться только точками оси ординат, поэтому прямая d' совпадает с прямой х = 0 , что имеет место лишь при a ₁₁ ≠ 0, a ₁₂ = a ₁ = 0.

Тождество F(x, у)=a ₁₁ x ² , а вместе с тем и разбираемый частный случай теоремы доказаны.

Пусть теперь кривая, определяемая уравнением (1), не есть пара совпадающих прямых. Тогда на ней можно найти пять точек M₁ , M₂ , M₃ , M₄ , M₅ , из которых никакие четыре не лежат на одной прямой. Это очевидно, если кривая (3) нераспадающаяся: тогда никакие три ее точки не лежат на одной прямой, и, следовательно, в качестве точек M₁ , M₂ , M₃ , M₄ , M₅ можно взять любые пять точек, удовлетворяющих уравнению (3). Если же кривая (3) распадается па пару различных прямых d и d ′ , то достаточно взять три точки на одной из этих прямых, а две другие — на другой. Точки (из которых никакие четыре не лежат на одной прямой) лежат и на кривой (3), и на кривой (4); поэтому, в силу теоремы, левые части уравнений (3)и(4) могут отличаться лишь постоянным множителем. Теорема 2 доказана.

Если (3) не есть мнимый эллипс или пара мнимых (сопряженных) прямых, т. е. если она содержит более одной действительной точки, то множество ее действительных точек бесконечно, и поэтому точки M₁ , M₂ , M₃ , M₄ , M₅ в предыдущем рассуждении могут быть предположены действительными. Этим доказано и добавление к теореме 2 .

2 Разные способы доказательства теоремы единственности

Преимущество предлагаемого второго доказательства заключается в том, что оно легко может быть перенесено на случай поверхностей F{x, у, z) = 0 (и даже на случай ( n -1) - мерных поверхностей второго порядка в n -мерном пространстве).

Обозначим через C множество точек, лежащих на кривой

F(x, у) = а₁₁ х² + 2а₁₂ ху + а₂₂ у² + 2а₁ х + 2а₂ у + а₀ = 0 (6)

т. е. множество всех точек М=(х,у) комплексной плоскости, удовлетворяющих уравнению (6). Предположим, что множество С совпадает с множеством всех точек комплексной плоскости, удовлетворяющих уравнению

F (x, y) = b₁₁ x² + 2b₁₂ xy + b₂₂ y² + 2b₁ x + 2b₂ y + b₀ = 0 (7)

Вспомним, что неасимптотические направления {α : β} по отношению к кривой (6) характеризуются тем, что имеется прямая данного направления {α : β} имеющая с множеством С ровно две (различные) общие точки, поэтому всякое направление, неасимптотическое для одной из двух кривых (6) и (7), будет неасимптотическим и для другой кривой.

Выбираем некоторое определенное неасимптотическое направление {α : β} для кривых (6) и (7).

Одну из прямых dнаправления {α : β} примем за ось ординат, а диаметр, сопряженный направлению {α : β}, — за ось абсцисс координатной системы О'х'у'. Из результатов предыдущего параграфа следует, что уравнения (3), (6) получат в системе координат О'х'у'